Pada bab ini dijelaskan mengenai pendugaan niai-tengah populasi, yaitu pusat data yang paling sering dibahas. Dalam pembahasan ini, peubah yang dibicarakan adalah berupa peubah pengukuran yang diasumsikan memiliki sebaran normal.
6.1 Kesahihan Asumsi Sebaran Normal
Sebaran normal adalah sebaran kontinu dengan domain (x) mengambil nilai mulai dari -∞ sampai dengan +∞.
µ dan σ adalah rata-rata populasi dan standar deviasi.
Untuk peubah pengukuran, asumsi sebaran Normal ini sesuai dengan anggapan dasar tentang sebaran data yang simetrik dengan frekuensi kelas yang semakin kecil dengan semakin jauhnya kelas tersebut dari pusat data.
Laju penurunan nilai fungsi dengan semakin jauhnya x dari pusat data juga cukup sesusai sehingga peluang suatu selang ekstrim masuk dalam populasi yang dibicarakan praktis mendekati nol.
Contoh Soal 6.1
1. Jika tinggi badan orang Indonesia diasumsikan bersebaran Normal dengan µ = 165cm dan σ = 10cm misalnya, maka berapakah peluang x kurang dari 135cm atau lebih dari 195cm?
Penyelesaian:
µ = 165cm
σ = 10cm
x1 = 135cm
x2 = 195cm
sehingga,
= (- 0.0013) + 0.9987 (nilai tersebut di lihat berdasarkan tabe ditribusi normal)
= 0.9974
2. Jika x adalah ditribusi normal dengan µ = 5, dan σ = 2. Hitunglah P (x > 7).
Penyelesaian:
3. bobot paket daging sapi yang terdistribusi normal dengan mean 1 pound dan deviasi standar 10. Berapakah peluang bahwa sebuah paket yang dipilih secara acak yang mempunyai berat antara 0.80 dan 0.85 pound?
6.2 Rataan Contoh
Pada bab sebelumnya telah di pelajari bahwa nilai harapan rataan contoh adalah sama dengan nilai harapan peubah asalnya:
Untuk mengulas kembali nilai harapan dapat dijelaskan sebagai berikut, sebaran (distribusi) peluang (probabilitas) memiliki berbagai sifat atau karakteristik yang dapat digunakan untuk mengidentifikasi suatu distribusi. Karakteristik yang biasa digunakan antara lain rata-rata hitung yang biasa disebut “harapan matematis” (atau nilai harapan) dan variansi. Harapan matetatis ini menentukan tendensi sentral dari distribusi probabilitas.
Rata-rata perubah acak X atau rata-rata distribusi peluang X. Dalam statistik rata-rata ini disebut harapan matematik atau nilai harapan dari perubah acak X, dinyatakan sebagai rata-rata atau nilai harapan dari perubah acak X ini menggambarkan letak pusat distribusi probabilitas.
Dengan demikian rataan contoh dapat dikatakan sebagai penduga tak bias bagi nilai-tengah populasi. Pendugaan adalah proses yang menggunakan sampel statistik untuk menduga atau menkasir hubungan parameter populasi yang tidak diketahui. Penduga adalah suatu statistik yang digunakan untuk menduga parameter. Jika suatu penduga dikatakan tidak bias bagi parameternya apabila penduga sama dengan nilai yang diduganya (parameter). E (penduga) = Parameter. Penduga tersebut secara tepat dapat menduga nilai parameternya.
Selanjutnya, selain tidak bias, dapat ditunjukan pula bahwa nilai tengah ini merupakan penduga yang paling efisien dan konsisten. Suatu penduga tak bias dikatakan sebagai penduga yang paling efisien apabila penduga tersebut ragamnya paling kecil dibandingkan dengan penduga tak bias lainnya.
 jelas lebih kecil dari ragam X (ragam individu)
jelas lebih kecil dari ragam X (ragam individu) Dengan simulasi, ragam percontohan bagi nilai-tengah juga dapat ditunjukan lebih kecil dari ragam percontohan median. Secara matematis, dapat pula ditunjukan bahwa ragam rataan contoh merupakan ragam minimum.
Rataan dikatakan demikian sebagai penduga yang konsisten bagi µ, yaitu bahwa dengan semakin besarnya ukuran contoh, n, nilai dugaannya semakin dekat dengan µ yang di duga.
6.3 Selang Kepercayaan Bagi Nilai-Tengah (Pendugaan Parameter)
Walaupun nilai harapan rataan contoh sama dengan nilai-tengah populasi, menyatakan nilai-tengah populasi sama dengan rataan contoh jelas salah. Nilai-tengah populasi adalah suatu nilai tetap, sedangkan rataan contoh tidak tetap.
Berdasarkan rataan contoh kita dapat membuat pernyataan bahwa nilai tengah populasi tersebut termasuk di dalam suatu selang angka tertentu dengan tingkat kepastian tertentu. Selang tersebut dikenal sebagai selang kepercayaan.
Selang kepercayaan bagi nilai-tengah populasi, µ, adalah selang dugaan yang kedalamnya diharapkan tercakup nilai µ. Besarnya harapan bahwa selang tersebut benar mencakup nilai µ dinyatakan sebagai tingkat kepercayaan yang dipasang pada selang tersebut, yang besarnya dinyatakan sebagai (1-α)100%. Selang kepercayaan (1-α)100% menunjukkan selang dugaan yang peluang bahwa nilai A dan B masing-masing adalah batas atas dan batas bawah selang kepercayaan (1-α)100% maka
6.3.1 Contoh Besar
Untuk menduga nilai tengah populasi dari suatu contoh yang diambil dari populasi yang menyebar normal dimana σ diketahui maka digunakan grafik seperti berikut :
Selang kepercayaan tersebut juga berlaku untuk populasi yang menyebar normal atau hampir normal jika n lebih dari sama dengan 30 dimana σ tidak diketahui. Dalam hal demikian nilai s digunakan sebagai nilai σ pada perhitungan.
Contoh Soal 6.3.1
1. Perusahaan A dan B menguji kekuatan 25 ban. Kekuatan rata-rata yang diperoleh adalah 13,5 satuan kekuatan tarik. Populasi ban dianggap menyebar normal dengan simpangan baku 0,8 satuan kekuatan. Buat selang kepercayaan untuk ukuran kekuatan rata-rata populasi ban pada tingkat kepercayaan 95% dan 99% !
Penyelesaian:
Diketahui : σ = 0,8
n = 25
populasi menyebar normal
2. Apabila suatu contoh acak berukuran 35 ditarik dari suatu populasi dan diperoleh nilai tengah contoh sebesar 40 dan simpangan baku 5, maka selang kepercayaan 95% bagi nilai tengah populasi tersebut adalah?
Peneyelesaian:
Diketahui:  =40
=40 Pendugaan parameter
Pendugaan dapat dilakukan dengan dua metode yaitu Metode Klasik dan Metode Bayes. Pada bagian ini digunakan pendugaan metode Klasik. Pengambilan keputusan di Metode Klasik hanya didasarkan pada informasi yang diperoleh dari suatu contoh acak yang ditarik dari suatu populasi.
Contoh :
Buat selang kepercayaan 90% untuk isi rata-rata suatu makanan ringan yang dihasilkan dari mesin otomatis. Jika isi rata-rata 16 bungkus contoh adalah 0,25 gr dengan simpangan baku 0,075 gr. Asumsikan populasi menyebar hampir normal.
Jawab :
Contoh :
Makanan ringan hasil pengisian dengan mesin diketahui menyebar normal dengan simpangan baku 8 gr. Untuk mengetahui nilai tengah isi bungkus makanan ringan pada periode pengisian akan dibuat selang kepercayaan sebesar 99% yang besarnya 10 gr maka ukuran contoh yang perlu ditarik adalah........
Contoh :
Berikut adalah tabel hasil pengamatan berpasangan pria dan wanita pembaca koran di beberapa kota.
Jumlah pembaca koran | |||||
Pria | 30 | 35 | 40 | 15 | 50 |
Wanita | 25 | 30 | 35 | 10 | 45 |
Buat selang kepercayaan 95% keduanya!
Jawab :
Pria (X1) | Wanita (X2) | B = (X1) - (X2) |
30 | 25 | 5 |
35 | 30 | 5 |
42 | 35 | 7 |
15 | 10 | 5 |
54 | 45 | 9 |
DAFTAR PUSTAKA
Anto Dajan. 1986. Pengantar Metode Statistik. Jilid II. Jakarta: PT. Pustaka LP3ES Indonesia.
Budi, Santosa. 2007. Statistika Deskripftif. Jakarta : Erlangga
Budiman, Chandra. 1995. Pengantar statistic kesehatan. Jakarta : EGC
Gunawan, Ellen. 2005. Teknik Statistika untuk Bisnis dan Ekonomi. Jakarta : Erlangga
J. Supranto. 2001. Statistik: Teori dan Aplikasi Jilid 2.Edisi Keenam. Jakarta: Erlangga.
Murray R. Spiegel dan I Nyoman Susila. 1984. Statistik. Jakarta: Erlangga.
Rasyad, Rasdihan. 2007. Metode Statistik Deskfriptif. Jakarta : Grasindo
Ronald E. Walpole dan Raymond H. Myers. 1995. Ilmu Peluang dan Statistika untuk Insinyur dan Ilmuan Terjemahan oleh RK. Sembiring. Bandung: ITB Bandung.
Saefuddin, Asep. 2007. Statistika Dasar. Jakarta : Grasindo
Spiegel, Murray R. 2007. Schaum’s Outlines. Jakarta : Erlangga
Supranto. 2000. Statistik Teori dan Aplikasi. Jakarta: Erlangga
Sutrisno Hadi. 2004. Statistik Jilid 1. Yogyakarta: Andi Yogyakarta
Sumber internet:


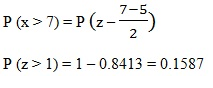





















Tidak ada komentar:
Posting Komentar