KORELASI DAN REGRESI LINEAR SEDERHANA
1. Korelasi
Pada semua kejadian, baik kejadian ekonomi maupun lainnya, pasti ada faktor yang menyebabkan terjadinya kejadian-kejadian tersebut. Misal, angka penjualan suatu barang yang turun disebabkan oleh naiknya harga barang tersebut. Contoh lain, seorang anak yang tidak belajar mendapatkan nilai jelek pada saat ulangan, dll.
Uraian di atas menunjukkan adanya hubungan atau korelasi antara kejadian yang satu dengan kejadian yang lainnya. Kejadian itu dapat dinyatakan dengan perubahan nilai variabel. Misal, jika x merupakan variabel harga, maka naik turunnya harga dapat dinyatakan dengan perubahan nilai x. Dan apabila y merupakan variabel hasil penjualan, maka naik turunnya hasil penjualan dapat dinyatakan dengan perubahan nilai y. Jadi, hubungan antara dua kejadian dapat dinyatakan dengan hubungan dua variabel x dan y. Disini saya hanya akan menjelaskan tentang hubungn antara dua variabel, hubungan linier lebih dari dua variabel akan dijelaskan pada subbab berikutnya.
Pada contoh diuraian sebelumnya, kita tentu setuju jika dikatakan bahwa naik turunnya harga mempengaruhi hasil penjualan. Namun dalam hal ini kita tidak tahu pasti seberapa besar pengaruhnya. Analisis korelasi yang akan dibahas kali ini berfungsi untuk mengetahui seberapa besar atau seberapa kuat suatu relasi antar dua variabel.
2. Ukuran korelasi
Hubungan dua variabel ada yang positif dan negatif. Suatu hubungan dikatakan positif apabila kenaikan/penurunan x pada umumnya diikuti oleh kenaikan/penurunan y. Sebaliknya dikatakan negatif bila kenaikan/penurunan x pada umumnya diikuti oleh penurunan/kenaikan y. Perhatikan Gambar 1 dan 2.
Gambar 1. Korelasi positif
Gambar 2. Korelasi negatif.
Contoh korelasi positif:
x = pupuk, y = produksi
x = biaya iklan, y = hasil penjualan
x = berat badan, y = tekanan darah
Contoh korelasi negatif:
x = harga suatu barang, y = permintaan barang
x = pendapatan masyarakat, y = kejahatan ekonomi
Apabila diagram pencar tidak teratur, artinya kenaikan/penurunan x tidak berpengaruh pada kenaikan/penurunan x. Maka dapat dikatakan x dan y tidak berkorelasi.
3. Koefisien korelasi
Kuat dan tidaknya hubungan antara x dan y apabila dinyatakan denagn fungsi linier, diukur dengan suatu nilai yang disebut koefisien korelasi (r). Nilai koefisien korelasi ini paling sedikit bernilai -1 dan paling besar bernilai 1. Jadi dapat dinyatakan sebagai berikut:
-1<= r >= 1
Artinya:
· Jika r = 1, hubungan x dan y sempurna dan positif (mendekati 1, yaitu hubungan sangat kuat dan positif).
· Jika r = -1, hubungan x dan y sempurna dan negatif (mendekati -1, yaitu hubungan sangat kuat dan negatif).
· Jika r = 0, tidak ada hubungan atau lemah sekali hubungan antara x dan y.
Cara menghitung nilai r yakni:
Rumus ini merupakan rumusan koefisien korelasi Pearson.
4. Koefisien Penentu
Nilai x dikatakan mempengaruhi y karena kenaikan atau penurunan x mempengaruhi nilai y. Namun dalam diagram pencar, nilai y memiliki nilai yang bervariasi meskipun nilai y naik dalam deret ukur. Hal ini terjadi karena nilai y tidak hanya dipengaruhi oleh variabel x namun juga beberapa faktor lain. Misal, hasil penjualan tidak hanya dipengaruhi oleh harga pasar tapi melainkan juga dipengaruhi oleh pendapatan masyarakat, selera, dll. Dari sini timbul pertanyaan, beraa besarnya kontribusi dari x terhadap naik turunnya nilai y? Untuk menjawab pertanyaan ini harus dihitung dulu suatu koefisien yang disebut keofisien determinasi atau koefisien penentu (KP). Nilai KP dicari dengan rumus,
KP = r2
Jika r = 0.9 maka nilai KP = (0.9)2 = 0.81 atau 81%. Hal ini berarti besar kontribusi dari x terhadap nilai y sebesar 81%, dan 19% lainnya adalah kontribusi dari faktor-faktor lainnya.
Contoh soal korelasi:
- Jika x adalah presentase kenaikan biaya iklan dan y adalah presentase kenaikan hasil penjualan, kemudian berdasarkan tabel dibawah ini, hitunglah koefisien korelasi (r)!
x | 1 | 2 | 4 | 5 | 7 | 9 | 10 | 12 |
Y | 2 | 4 | 5 | 7 | 8 | 10 | 12 | 14 |
Penyelesaian :
untuk menghitung r diperlukan lembaran kerja yang disusun berdasarkan rumus sebagai berikut :
x | Y | x2 | y2 | xy |
1 | 2 | 1 | 4 | 2 |
2 | 4 | 4 | 16 | 8 |
4 | 5 | 16 | 25 | 20 |
5 | 7 | 25 | 49 | 35 |
7 | 8 | 49 | 64 | 56 |
9 | 10 | 81 | 100 | 90 |
10 | 12 | 100 | 144 | 120 |
12 | 14 | 144 | 196 | 168 |
Σxi = 50 | Σyi = 62 | Σxi2 = 420 | Σyi2 = 598 | Σxiyi = 499 |
2. 2. Jika X adalah presentase kenaikan harga dan Y adalah presentase kenaikan hasil penjualan, kemudian berdasarkan tabel dibawah ini, hitunglah koefisien korelasi (r) dan kofisien determinasi (KP) !
X | 2 | 4 | 5 | 6 | 8 | 10 | 11 | 13 | 14 | 15 |
Y | 15 | 14 | 12 | 10 | 9 | 8 | 6 | 4 | 3 | 2 |
Penyelesaian :
untuk menghitung r diperlukan lembaran kerja yang disusun berdasarkan rumus sebagai berikut :
X | Y | X2 | Y2 | XY |
2 | 15 | 4 | 225 | 30 |
4 | 14 | 16 | 196 | 56 |
5 | 12 | 25 | 144 | 60 |
6 | 10 | 36 | 100 | 60 |
8 | 9 | 64 | 81 | 72 |
10 | 8 | 100 | 64 | 80 |
11 | 6 | 121 | 36 | 66 |
13 | 4 | 169 | 16 | 52 |
14 | 3 | 196 | 9 | 42 |
15 | 2 | 225 | 4 | 30 |
ΣXi=88 | ΣYi=83 | ΣXi2= 956 | ΣYi2=875 | ΣXiYi=548 |
Kesimpulan: hubungan X dan Y kuat dan negatif. Dengan demikian, nilai KP = r2 = (-0.99)2 = 0.9801 = 0.98 = 98%.
5. Regresi
Apa perlunya mengetahui hubungan antar variable? Di dalam perencanaan, selain data masa lampau dan masa sekarang, juga diperlukan data hasil ramalan yang menggambarkan kemampuan di masa yang akan datang. Misalnya, perusahaan dalam merencanakanproduksi memerlukan ramalan hasil penjualan (kemampuan menjual di masa yang akan datang, sehingga dapat dicegah terjadinya overproduction atau underproduction).
Apabila dua variable X dan Y mempunyai hubungan, maka nilai variable X yang sudah diketahui dapat digunakan untuk menaksir/memperkirakan nilai variable Y.
Variable Y yang nilainya akan diramalkan disebut variable tidak bebas (dependent variable), sedangkan variable X yang nilainya digunakan untuk meramalkan nilai Y disebut variable bebas (independent variable).
Jadi analisis korelasi membantu kita untuk mengetahui seberapa kuat hubungan antara dua variable, sedangkan analisis regresi membantu kita untuk:
1. Mengetahui apakah ada relasi/hubungan antar variable
2. Membantu menentukan jenis persamaan yang akan digunakan untuk menentukan hubungan tersebut..
6. Diagram pencar
Jika terdapat sebuah data antara dua variable dan kita belum dapat memastikan apakah data tersebut memiliki hubungan satu sama lain atau tidak, cara untuk mengetahuinya adalah dengan cara menggunakan diagram pencar (scatter diagram).
Gambar 3. Macam-macam scatter diagram
Pada kesempatan ini hanya akan dijelaskan mengenai regresi linear sederhana yakni regresi yang berbentuk garis lurus atau linear (gambar (a), dan (b)).
7. Persamaan Regresi Linear Sederhana
Bentuk umum persamaan regresi linier: y = a + bx
y : peubah takbebas x : peubah bebas
a : konstanta b : kemiringan/gradien
· Penetapan Persamaan Regresi Linier Sederhana
Dengan, n : banyak pasangan data
yi : nilai peubah takbebas y ke-i
xi : nilai peubah bebas x ke-i
Contoh soal regresi linear sederhana:
1. Berikut adalah data Biaya Promosi dan Volume Penjualan PT BIMOIL perusahaan Minyak Goreng. Banyaknya data ada lima data. Tentukan persamaan regresinya!
Tahun | x Biaya Promosi (Juta Rupiah) | Y Volume Penjualan (Ratusan Juta Liter) | xy | x² | y² |
1992 | 2 | 5 | 10 | 4 | 25 |
1993 | 4 | 6 | 24 | 16 | 36 |
1994 | 5 | 8 | 40 | 25 | 64 |
1995 | 7 | 10 | 70 | 49 | 100 |
1996 | 8 | 11 | 88 | 64 | 121 |
S | Sx = 26 | Sy = 40 | Sxy = 232 | Sx² =158 | Sy² = 346 |
bentuk umum persaman regresi linier sederhana : y = a + b x
y = a + b x ® y = 2.530 + 1.053 x
2. Diketahui hubungan Biaya Promosi (x dalam Juta Rupiah) dan y (Volume penjualan dalam Ratusan Juta liter) dapat dinyatakan dalam persamaan regresi linier berikut
y = 2.530 + 1.053 x. Perkirakan Volume penjualan jika dikeluarkan biaya promosi Rp. 10 juta ?
Penyelesaian: y = 2.530 + 1.053 x
x = 10
y = 2.53 + 1.053 (10) = 2.53 + 10.53 = 13.06 (ratusan juta liter)
Volume penjualan = 13.06 x 100 000 000 liter
8. Standar Error Estimasi
Dalam menggunakan persamaan regresi untuk melakukan suatu perkiraan, terdapat satu pertanyaan penting mengenai seberapa kuat hubungan antar variable bebas dan terikatnya; atau dengan kata lain, seberapa besar derajat ketergantungannya (dependability) hasil perkiraan tersebut. Hal ini dapat lebih dimengerti dengan memperhatikan gambar 4 (a), terlihat bahwa titik-titik data terpencar lebih rapat di sekitar garis regresi dibandingkan dengan titik-titik data pada gambar 4 (b). Dengan nalar secara awam saja, kita dapat mengatakan bahwa suatu estimasi yang dilakukan dengan persamaan garis regresi untuk keadaan pada gambar 4 (a) akan lebih baik dibandingkan untuk keadaan pada gambar 4 (b).
Gambar 4
Ukuran yang mengindifikasi derajat variasi sebaran data di sekitar garis regresi dapat menunjukkan seberapa besar derajat keterikatan perkiraan yang diperoleh dengan menggunakan persamaan regresi tersebut. Ukuran ini dinamakan sebagai standar error estimasi. Dalam definisi yang lebih tepat standar error estimasi estimasi (sy,x) adalah deviasi standar yang memberikan ukuran penyebaran nilai-nilai yang teramati di sekitar garis regresi, dirumuskan sebagai berikut:
Contoh soal:
Dari suatu praktikum fisika dasar diperoleh data yang menghubungkan variabel bebas x dan variabel terikat y seperti ditunjukkan dalam tabel berikut:
Ujian ke- | x | y |
1 | 6 | 30 |
2 | 9 | 49 |
3 | 3 | 18 |
4 | 8 | 42 |
5 | 7 | 39 |
6 | 5 | 25 |
7 | 8 | 41 |
8 | 10 | 52 |
S | 56 | 296 |
Jika diasumsikan memiliki bentuk hubungan yang linear, maka hitunglah persamaan garis regresinya dan standar error estimasinya!
Penyelesaian:
Ujian ke- | x | y | xy | x2 | y2 |
1 | 6 | 30 | 180 | 36 | 900 |
2 | 9 | 49 | 441 | 81 | 2401 |
3 | 3 | 18 | 54 | 9 | 324 |
4 | 8 | 42 | 336 | 64 | 1764 |
5 | 7 | 39 | 273 | 49 | 1521 |
6 | 5 | 25 | 125 | 25 | 625 |
7 | 8 | 41 | 328 | 64 | 1681 |
8 | 10 | 52 | 520 | 100 | 2704 |
S | 56 | 296 | 2257 | 428 | 12920 |
· Nilai konstanta b dapat ditentukan:
· Nilai konstanta a dapat ditentukan:
Jadi persamaan regresi linear yang menggambarkan hubungan antara variabel x dan y dari data sampel pada percobaan/praktikum di atas adalah:
y = 1.0277 + 5.138 x
· Menghitung standar error estimasi:
Perkiraan atau Pendugaan Interval
Pada teori pendugaan (estimation theory) terdapat dua hal yang penting yaitu pendugaan interval (confidence interval, atau interval estimation) dan pendugaan tunggal (prediction interval atau point estimation). Pendugaan interval dimaksudkan untuk menggambarkan nilai tengah untuk setiap nilai X tertentu, sedang pendugaan tunggal untuk menggambarkan kisaran nilai untuk setiap nilai X tertentu.
1.1 Pendugaan Nilai – Tengah Y.
Pendugaan interval nilai tengah Y dimaksudkan untuk mengetahui nilai dugaan bagi Y untuk seluruh nilai X yang diketahui. Telah disinggung pada sub-bab sebelumnya bahwa dalam model regresi linier ini, dengan adanya nilai pengamatan dari nilai dugaannya, suatu nilai peubah bebas X tertentu dapat memberikan beragam nilai peubah Y yang bervariasi yang pusatnya diperkirakan terletak pada titik yx = β0 + β1x. Dengan kata lain, nilai harapan Y pada X tertentu adalah β0 + β1X. Nilai tengah Y tersebut diduga oleh y = b0 + b1x dengan galat baku:
Contoh 1
Berikut ini adalah delapan pengukuran pada tinggi anak dengan tinggi bapak dan tinggi anak sulungnya (cm).
Tentukan selang kepercayaan 95% bagi nilai-tengah tinggi badan anak yang bapaknya memiliki tinggi 165 cm!
Jawab:
Untuk pengamatan tersebut dapat dibuat tabel berikut ini (X untuk tinggi bapak, Y untuk tinggi anak)
Model Regresinya adalah:
sehingga Y = 64.70 + 0.623x
Penduga titik nilai – tengah tinggi anak yang bapaknya memiliki tinggi 165 cm adalah:
µy|x=165 = 64.70 + (0.623) (165) = 167.495 cm
Galat baku dugaan tersebut adalah:
dengan t0.025,6 = 2.447
Selang kepercayaan 95% tinggi anak yang bapaknya memiliki tinggi 165 cm adalah :
1.2. Pendugaan Satu Nilai y pada x tertentu (Pendugaan Tunggal)
Nilai y pada x tertentu juga diduga dengan y = b0 + b1x. Berbeda dengan nilai tengahnya, galat baku pendugaan satu nilai y adalah 
sehingga selang kepercayaan (1 - α) 100% bagi y pada x tertentu adalah
Contoh 2
Untuk data pada contoh 1 tentukan selang kepercayaan 95% bagi tinggi badan seorang anak yang bapaknya memiliki tinggi 165 cm!
Jawab:
Penduga titik nilai y pada tinggi anak yang bapaknya memiliki tinggi 165 cm adalah
y|x=165 = 64.70 + (0.623) (165) = 167.495 cm
Galat baku dugaan tersebut adalah:
dengan t0.025,6 = 2.447
Selang kepercayaan 95% tinggi anak yang bapaknya memiliki tinggi 165 cm adalah :
Tabel Analisis Ragam
Analisis ragam atau analysis of variance(ANOVA) adalah suatu metode untuk
menguraikan keragaman total data menjadi komponen-komponen yang mengukur
berbagai sumber keragaman. Pengujian model dapat juga dilakukan dengan menggunakan analisis ragam. Perhatikan bahwa jumlah kuadrat total dapat diuraikan menjadi jumlah kuadrat regresi dan jumlah kuadrat galat sebagai berikut:
Sementara itu, derajat bebas masing – masing jumlah kuadrat tersebut berturut – turut adalah:
DB(Total) = n – 1
DB(Regresi) = 1
DB(Galat)= n-2
Sedangkan DB(Total)= DB(Regresi) + DB(Galat)
Tabel Analisis dengan demikian dapat disusun, sebagai berikut:
Nilai Fhitung dari table analisis raga mini adalah nilai F uji atas hipotesis H0 : σ2regresi = σ2sisa v.s. H1 : σ2regresi = σ2sisa
Nilai Fhitung yang lebih dari Fα, DB(Regresi),DB(Galat) yang berarti tertolaknya H0 pada taraf nyata α, diinterpretasikan bahwa persamaan regresi linear yang terpasang pada data adalah berperan dalam menjelaskan keragaman total. Dengan kata lain, tertolaknya H0 dalam uji-F tadi menunjukkan adanya peran peubah bebas dalam menjelaskan keragaman peubah tak bebas, atau keragaman data bukanlah sekedar keragaman acak tetapi berkaitan dengan keragaman peubah bebas menurut persamaan regresi linier.
Contoh 3
Untuk data pada contoh 1 buatlah tabel analisis ragam untuk regresi tinggi badan anak pada tinggi badan bapaknya!
Jawab :
Untuk data pada contoh 1 dapat disusun tabel perhitungan sebagai berikut :
Dari tabel diperoleh:
JK (Galat) = 375.80
JK (Total) = 463.50
JK (Regresi) = JK(Total) – JK (Galat)
= 463.50 – 375.80
= 87.7
Tabel Analisis Ragam untuk regresi tinggi badan anak pada tinggi badan bapaknya :
Adapun F0.05,1.6 = 5.99
Dengan Fhitung tidak lebih dari F0.05,1.6 maka keputusan ujinya adalah tidak tolak H0. Berdasarkan data tabel tersebut , persamaan regresi linier yang terpasang pada data belum bisa dikatakan berperan dalam menjelaskan keragaman total.
Kesesuaian Model Regresi
Kesesuaian model merupakan ukuran untuk mengetahui kesesuain atau ketepatan antara nilai dugaan atau garis regresi dengan data sample. Ukuran kesesuaian model ini disebut Koefisien Determinasi (R2). Koefisien Determinasi adalah bagian dari keragaman total variable tak bebas Y (variable yang dipengaruhi atau dependent) yang dapat diterangkan atau diperhitungkan oleh keragaman variable bebas X (variabel yang mempengaruhi atau independent). Jadi koefisien determinasi adalah kemampuan variable X (variable independent) mempengaruhi variable Y (variable dependent). Semakin besar koefisien determinasi menunjukan semakin baik kemampuan X menerangkan Y. Besarnya koefisien determinasi adalah kuadrat dari koefisien korelasi dan dirumuskan sbb :
Nisbah kuadrat tengah total pada kuadrat tengah galat menunjukkan besarnya keragaman data yang tidak terjelaskan oleh model. Koefisien determinasi dengan demikian menyatakan besarnya keragaman yang terjelaskan oleh model. Nilai minimum koefisien determinasi adalah 0, dan nilai maksimumnya adalah 1. Semakin besar nilai koefisien determinasi, mendekati angka 1, semakin sesuai model yang dipasang dengan data yang dibicarakan. Koefisien determinasi kadang – kadang juga dinyatakan dalam persen, sehingga nilainya berkisar antara 0 – 100%.
Contoh 4
Hitunglah besarnya koefisien determinasi untuk regresi tinggi badan anak pada tinggi badan bapaknya!
Jawab:
Dari contoh 1, koefisien determinasi regressi tersebut adalah:
Koefisien determinasi untuk model regresi ini sangat kecil, menunjukkan model ini kurang baik dalam menjelaskan keragaman peubah respon dalam kaitannya dengan peubah penjelas. Kurang baiknya model ini mungkin karena antara kedua peubah tersebut pada kenyataannya tidak berkaitan satu sama lain, atau keterkaitan antara peubah tersebut ada tetapi tidak linier.
REGRESI GANDA
I. Pengertian Regresi Ganda
Regresi ganda adalah regresi suatu variable terikat yang memiliki lebih dari satu variable bebas. Bentuk persamaan umum dari regresi ganda adalah :
Regresi ganda berguna untuk mencari pengaruh dua variable predictor atau untuk mencari hubungan fungsional dua variable penjelas (variable bebas) atau lebih terhadap variable respon(variable terikat). Penyelesaian regresi ganda dapat menggunakan notasi matriks dan persamaan linear dengan metode substitusi dan eliminasi.
II. Metode Regresi Ganda
a. Metode Matriks
Dalam notasi matriks, p merupakan variable bebas berdasarkan jumlah pengamatan (n):
Dengan
Y = vector variable terikat berukuran nX1
X = matriks variable bebas berukuran n X (p+1)
beta = vector koefisien regresi berukuran (p+1) X 1
Pendugaan koefisien regresi di buat dengan cara mendapatkan solusi atas persamaan normal yaitu
Sehingga
Selanjutnya ragan bagi beta , s2{b}, dalam notasi matriks dituliskan sebagai :
dengan
Dapat di buat dengan criteria uji T. Tolak H0 jika t lebih kecil atau sama dengan -ta/2,n-(p+1) atau sama dengan -ta/2,n-p dengan t = be / s{bk} , P(T ³ -ta/2,n-(p+1)) = a/2, dan
Pendugaan Nilai Peubah Respon galat baku bagi dugaan nilai-tengah Y dan dugaan nilai Y pada X tertentu, Xt’ dalam bentuk matriks masing-masing adalah :
Selang kepercayaan (1-a) 100% bagi nilai tengah Y dan dugaan nilai Y pada X tertentu , Xt' masing-masing adalah:
Jumlah kuadrat total, jumlah kuadrat regresi dan jumlah kuadrat galat dalam matriks ditulis masing-masing sebagai berikut:
Derajat bebas yang berpadanan dengan masing-masing jumlah kuadrat tersebut adalah :
Koefisien determinasi yang merupakan ukuran kesesuaian model dapat dihitung yaitu:
a. Metode Persamaan Linear
Persamaan regresi ganda dapat digunakan dalam perhitungan nilai Y untuk setiap perhitungan nilai X1dan X2. Perubahan nilai Y disebabkan oleh perubahan X1, ketika X2 konstan ataupun sebaliknya. Data pada table regresi, yang terdiri dari variable X1, X2, dan Y dapat di hitung dengan persamaan sebagai berikut:
Persamaan regresi ganda dapat di uji dengan persamaan berikut ini:
Kemudian mencari Rhintung dengan rumus:
Setelah Rhintung diperoleh maka kuadratkanlah Rhintung. Kemudian menghitung F sign hitung dengan rumus:
Contoh soal:
1. Diberikan data sebagai berikut:
Y | X1 | X2 |
23.3 | 5 | 13 |
24.5 | 6 | 14 |
27.2 | 8 | 17 |
27.1 | 9 | 17 |
24.1 | 7 | 14 |
23.4 | 5 | 13 |
24.3 | 6 | 14 |
24.1 | 7 | 14 |
27.2 | 9 | 17 |
27.3 | 8 | 17 |
27.4 | 8 | 17 |
27.3 | 9 | 17 |
24.3 | 6 | 14 |
23.4 | 5 | 13 |
24.1 | 7 | 14 |
27 | 9 | 17 |
23.5 | 5 | 13 |
24.3 | 6 | 14 |
27.3 | 8 | 17 |
23.7 | 7 | 14 |
Tentukan koefisien regresi X1, X2, dan Y dengan metode:
i) Persamaan linear
hitung pula nilai determinasi korelasiberganda dan F sign hitung
ii) Matriks
Penyelesaian:
Koefisien regresi X1, X2, dan Y
i) Persamaan linear
Buat table sebagai berikut:
No | Y | X1 | X2 | X1Y | X2Y | X1X2 | (X1)2 | (X2)2 | Y2 |
1 | 23.3 | 5 | 13 | 116.5 | 302.9 | 65 | 25 | 169 | 542.89 |
2 | 24.5 | 6 | 14 | 147 | 343 | 84 | 36 | 196 | 600.25 |
3 | 27.2 | 8 | 17 | 217.6 | 462.4 | 136 | 64 | 289 | 739.84 |
4 | 27.1 | 9 | 17 | 243.9 | 460.7 | 153 | 81 | 289 | 734.41 |
5 | 24.1 | 7 | 14 | 168.7 | 337.4 | 98 | 49 | 196 | 580.81 |
6 | 23.4 | 5 | 13 | 117 | 304.2 | 65 | 25 | 169 | 547.56 |
7 | 24.3 | 6 | 14 | 145.8 | 340.2 | 84 | 36 | 196 | 590.49 |
8 | 24.1 | 7 | 14 | 168.7 | 337.4 | 98 | 49 | 196 | 580.81 |
9 | 27.2 | 9 | 17 | 244.8 | 462.4 | 153 | 81 | 289 | 739.84 |
10 | 27.3 | 8 | 17 | 218.4 | 464.1 | 136 | 64 | 289 | 745.29 |
11 | 27.4 | 8 | 17 | 219.2 | 465.8 | 136 | 64 | 289 | 750.76 |
12 | 27.3 | 9 | 17 | 245.7 | 464.1 | 153 | 81 | 289 | 745.29 |
13 | 24.3 | 6 | 14 | 145.8 | 340.2 | 84 | 36 | 196 | 590.49 |
14 | 23.4 | 5 | 13 | 117 | 304.2 | 65 | 25 | 169 | 547.56 |
15 | 24.1 | 7 | 14 | 168.7 | 337.4 | 98 | 49 | 196 | 580.81 |
16 | 27 | 9 | 17 | 243 | 459 | 153 | 81 | 289 | 729 |
17 | 23.5 | 5 | 13 | 117.5 | 305.5 | 65 | 25 | 169 | 552.25 |
18 | 24.3 | 6 | 14 | 145.8 | 340.2 | 84 | 36 | 196 | 590.49 |
19 | 27.3 | 8 | 17 | 218.4 | 464.1 | 136 | 64 | 289 | 745.29 |
20 | 23.7 | 7 | 14 | 165.9 | 331.8 | 98 | 49 | 196 | 561.69 |
∑ | 504.8 | 140 | 300 | 3575.4 | 7627 | 2144 | 1020 | 4556 | 12795.82 |
Rata2 | 25.24 | 7 | 15 | 178.77 | 381.35 | 107.2 | 51 | 227.8 | 639.791 |
Dengan mensubstitusikan nilai masing-masing yang tertera pada table ke dalam persamaan di atas, sehingga:
504.8 = 20a + 140 b1 + 300 b2 ……………………………(1)
3575,4 = 140 a + 1020 b1 + 2144 b2 ……..………………(2)
7627 = 300 a + 2144 b1 + 4556 b2 ………………………… (3)
Eliminasi a dari persamaan (1) dan (2). Persamaan 1 dikalikan dengan -7 dan persamaan 2 dikalikan dengan 1
20a + 140 b1 + 300 b2 = 504.8 (x-7)
140 a + 1020 b1 + 2144 b2 = 3575,4 (x1)
sehingga diperoleh:
40 b1 + 44 b2 = 41.8 …………..(4)
• Eliminasi a dari persamaan (1) dan (3)
20a + 140 b1 + 300 b2 = 504.8 (x-15)
300 a + 2144 b1 + 4556 b2 = 7627 (x1)
Sehingga diperoleh :
44 b1 + 56 b2 = 55 ……………(5)
• Eliminasi persamaan (4) dan (5)
40 b1 + 44 b2 = 41.8 (x-44)
44 b1 + 56 b2 = 55 (x40)
Sehingga diperoleh b2 = 1.1868 dan b1 = 0.26
Maka nilai a dapat dihitung dengan rumus:
Maka a= 9.26
Sehingga
Y = 9.26 - 0.26 X1 + 1.1868 X2
ii) Matriks
Matriks di atas di inverskan
Sehingga diperoleh
Lalu dikalikan hasil invers diatas dengan X’Y
Menghasilkan
Dari matriks tersebut, maka diperoleh:
Y = 9.26 - 0.26 X1 + 1.1868 X2
Untuk data tersebut, KTG = 0.017 maka:
Sehingga
1. Untuk uji H0:bo = 0; H1:b1 ¹ 0;
2. Untuk H1:b = 0 ; H2: b ¹ 0,
3. Untuk H2: b = 0 ; H3: b ¹ 0,
Dengan t0.025;17 = 2.110 maka dapat disimpulkan untuk ketiga uji masing-masing adalah tolak Ho
2. Tentukan selang kepercayaan 95%bagi Yxt apabila X1 = 5 dan X2 = 14!
Jawab: Selang kepercayaan 95%
= 24.5742 ± (2.110) (0.017) (1+0.3395)
= 24.5262 atau 24.6222
3. Untuk data pada soal sebelumnya, buatlah tabel analisa ragam untuk regresi Y dengan dua variabel bebas
sumber | Jumlah Kuadrat | Derajat Bebas | Kuadrat Tengah | F hitung |
Regresi | 54.386 | 2 | 27.193 | 1641.14 |
Galat | 0.282 | 17 | 0.017 | |
Total | 54.668 | 19 |
Adapun F 0.025;17 = 3.59. dengan Fhitung jauh lebih besar dari F table, maka keputusan ujinya adalah tolak Ho.
4. Tentukan koefisien determinasi untuk model regresi linear Y pada peubah bebas X1 dan X2!
Jawab:
Ø Persamaan Linear
Persamaan regresi ganda dapat di uji dengan persamaan berikut ini:
Sehingga diperoleh
∑x1y = 41.8
∑x2y = 55
∑y2 = 54.668
Dari data tersebut juga dapat ditentukan nilai koefisien korelasi berganda yaitu dengan rumus:
sehingga R= 0.995207434
Ø Matriks
= 0.994235 = 99.42%
5. Tentukan nilai dari F hitung!
= 1765.08
dari data di atas, Ho dan Ha di tolak karena nilai F pada tabel adalah 3.59















































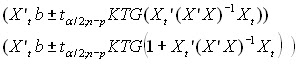

















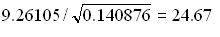







terima kasih, sangat membantuu sekalaiiiiii
BalasHapus