POPULASI DAN SAMPLING (PERCONTOHAN)
Populasi adalah keseluruhan obyek psikologis yang dibatasi kriteria-kriteria tertentu. Obyek psikologis bisa merupakan obyek yang bisa diraba atau konkret (tangible) maupun obyek abstrak (intangible). Misalnya, barang-barang manufakturing dan fisik orang merupakan contoh obyek yang bersifat konkret, sedangkan motivasi kerja, kesadaran hukum, atau kredibilitas seorang pemimpin merupakan contoh-contoh obyek yang bersifat abstrak. Dalam ilmu sosial, misalnya bisnis atau manajemen, obyek psikologis yang sering diteliti relatif lebih banyak bersifat abstrak.
Sampling adalah proses memilih obyek psikologis dari sebuah populasi tertentu. Segala sesuatu yang oleh peneliti dijadikan kesatuan (unit) yang nantinya akan menjadi obyek pemilihan tersebut disebut satuan sampling (sampling unit). Satuan sampling bentuknya bisa individu yang berdiri sendiri atau kumpulan individu. Misalnya, seorang konsumen, karyawan, keluarga, perusahaan, desa atau kelurahan, kota besar, dan sebagainya.
TEKNIK PENARIKAN SAMPEL (PERCONTOHAN)
- Penarikan Sampel Acak Sederhana (Simple Randomized Sampling)
Pengacakan dapat dilakukan dengan : undian, tabel bilangan acak, program komputer.
- Penarikan Sampel Sistematik (Systematic Sampling)
Tetapkan interval lalu pilih secara acak anggota pertama sampel
Contoh : Ditetapkan interval = 20
Secara acak terpilih : Anggota populasi ke-7 sebagai anggota ke-1 dalam sampel, maka : Anggota populasi ke-27 menjadi anggota ke-2 dalam sampel Anggota populasi ke-47 menjadi anggota ke-3 dalam sampel, dst.
- Penarikan Sampel Acak Berlapis (Stratified Random Sampling)
Populasi terdiri dari beberapa kelas/kelompok. Dari setiap kelas diambil sampel secara acak. Antar Kelas bersifat (cenderung) berbeda nyata (heterogen). Anggota dalam suatu kelas akan (cenderung) sama (homogen).
Contoh :
Dari 1500 penumpang KA (setiap kelas memiliki ukuran yang sama) akan diambil 150 orang sebagai sampel, dilakukan pendataan tentang tingkat kepuasan, maka sampel acak dapat diambil dari :
i. Kelas Eksekutif : 50 orang
ii. Kelas Bisnis : 50 orang
iii. Kelas Ekonomi : 50 orang
- Penarikan Sampel Gerombol/Kelompok (Cluster Sampling)
Populasi juga terdiri dari beberapa kelas/kelompok. Sampel yang diambil berupa kelompok bukan individu anggota. Antar Kelas bersifat (cenderung) sama (homogen). Anggota dalam suatu kelas akan (cenderung) berbeda (heterogen).
Contoh :
Terdapat 40 kelas untuk tingkat II Jurusan Ekonomi-GD, setiap kelas terdiri dari 100 orang. Populasi mahasiswa kelas 2, Ekonomi-UGD = 40 × 100 = 4000.
Jika suatu penelitian dilakukan pada populasi tersebut dan sampel yang diperlukan = 600 orang, dilakukan pendataan mengenai lama waktu belajar per hari maka sampel dapat diambil dari 6 kelas.... Dari 40 kelas, ambil secara acak 6 kelas.
- Penarikan Sampel Area (Area Sampling)
- Prinsipnya sama dengan Cluster Sampling.
- Pengelompokan ditentukan oleh letak geografis atau administratif.
- Contoh : Pengambilan sampel di daerah JAWA BARAT, dapat dilakukan dengan memilih secara acak KOTAMADYA tempat pengambilan sampel, misalnya terpilih, Kodya Bogor, Sukabumi dan Bandung,
Sampel acak menjadi dasar penarikan sampel lain. Selanjutnya, pembahasan akan menyangkut Penarikan Sampel Acak. Penarikan Sampel Acak dapat dilakukan dengan cara-cara berikut:
1. Berdasarkan aspek cara memilih dibagi menjadi:
(a) sampling dengan pengembalian.
Sampling dengan pengembalian apabila dalam proses pemilihannya, satuan sampling yang sudah terpilih dikembalikan lagi ke dalam populasi sebelum pemilihan berikutnya sehingga ada kemungkinan terpilih lebih dari sekali. Secara umum, jika dari populasi berukuran N diambil sampel berukuran n, maka semuanya ada 
buah sampel yang mungkin diambil.
buah sampel yang mungkin diambil.
(b) sampling tanpa pengembalian.
Sampling tanpa pengembalian apabila satuan sampling yang sudah terpilih tidak dikembalikan ke populasi sehingga tidak mungkin terpilih lebih dari sekali. Dalam prakteknya, tipe sampling tanpa pengembalian inilah yang paling sering digunakan. Secara umum, banyaknya sampel berukuran n yang dapat diambil dengan cara tanpa pengembalian dari sebuah populasi berukuran N adalah: 
- Berdasarkan Ukurannya, maka sampel dibedakan menjadi :
(a) Sampel Besar jika ukuran sampel (n) ≥ 30
(b) Sampel Kecil jika ukuran sampel (n) < 30
- Berdasarkan aspek peluang pemilihannya, sampling dikelompokkan menjadi dua tipe, yaitu:
(a) Sampling non peluang atau non probability sampling. Sampling dikatakan sampling non peluang jika dalam proses memilih satuan-satuan sampling tidak dilibatkan unsur peluang. Proses ini sangat sederhana dan tidak rumit tetapi mempunyai kerugian relatif besar yaitu tidak bisa dilakukan uji signifikansinya, artinya analisis inferensial secara statistic tidak valid
(b) Sampling peluang atau probability sampling/random sampling. Sampling peluang adalah sampling yang dalam proses pemilihan satuan-satuan samplingnya didasarkan pada unsur peluang sedemikian hingga peluang setiap satuan sampling untuk terpilih diketahui besarnya.
GAMBARAN TENTANG SUATU PERCONTOHAN
), yang diperoleh dari suatu percontohan (teknik pengambilan sampling). Hal ini menjadi dasar pembahasan pendugaan dan uji hipotesis tentang parameter lokasi peubah pengukuran.
Berikut akan dijelaskan penarikan sampel acak sederhana dengan pengembalian dan tanpa pengembalian.
- Penarikan sampel dengan pemulihan atau pengembalian.
Misalkan diketahui suatu populasi angka X = (3,4,6,9) dengan µ× = 5.5 dan σ2x = 7.0. Dari populasi tersebut misalkan ditarik contoh acak berukuran 2 dengan pemulihan. Maka dengan percontohan ini akan diperoleh 16 macam contoh yang masing-masing berpeluang sama untuk muncul. Untuk contoh-contoh tadi dapat dihitung rataannya masing-masing sehingga terbentuk sebaran peluang seperti tampak pada tabel 5-1.
Tabel 5-1 Contoh Berukuran Dua yang Diambil Secara Acak Dengan Pemulihan
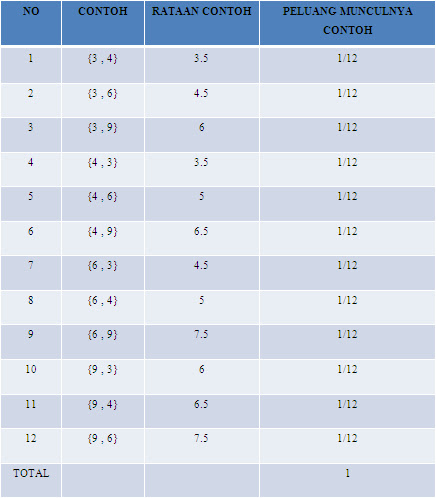
Dari sebaran sebelumnya kemudian dapat dibuat sebaran percontohan bagi rataan contoh, tampak pada Tabel 5-2.
Tabel 5-2 Sebaran Rataan Contoh Dari Tabel 5-1
Untuk percontohan dengan pemulihan dalam ilustrasi tadi, tampak bahwa
dan 
. Kesamaan ini secara matematis dapat ditunjukkan berlaku umum.
- Penarikan sampel tanpa pemulihan atau pengembalian.
Untuk populasi X={3,4,6,9} sebelumnya, apabila percontohannya dibuat tanpa pemulihan, maka contoh yang mungkin dengan rataan dan peluangnya masing-masing tampak pada Tabel 5-3.
Tabel 5-3 Contoh Berukuran Dua Yang Diambil Secara Acak Tanpa Pemulihan
Sebaran rataan dari percontohan tanpa pemulihan tampak pada Tabel 5-4.
Simpangan baku rataan dari percontohan demikian adalah akar kuadrat dari ragamnya, dinamakan sebagai galat baku percontohan:
 |
CONTOH SOAL
Jawab:
Tabel Contoh Berukuran Dua yang Diambil Secara Acak Dengan Pemulihan
Dari sebaran sebelumnya kemudian dapat dibuat sebaran percontohan bagi rataan contoh, tampak pada Tabel berikut.
Untuk populasi lima angka pada soal 1, tetapi penarikannya dilakukan tanpa pemulihan.
a. Daftarkan semua contoh berukuran 2 yang mungkin muncul dari percontohan tersebut, dan tentukan rataan dari masing-masing contoh tersebut!
Jawab:
Untuk populasi X={1,2,3,4} sebelumnya, apabila percontohannya dibuat tanpa pemulihan, maka contoh yang mungkin dengan rataan dan peluangnya masing-masing tampak pada Tabel berikut.
Tabel Contoh Berukuran Dua Yang Diambil Secara Acak Tanpa Pemulihan
Sebaran rataan dari percontohan tanpa pemulihan tampak pada berikut.
3. Contoh soal 5-3 Misalnya diketahui sebuah populasi dengan ukuran N=5 dengan satuan sampling lengkapnyaadalah A, B, C, D, dan E. Variabel yang diukur dari setiap satuan sampling tersebut adalah X dengan nilai-nilai X untuk setiap satuan sampling dapat dilihat pada Gambar 5 berikut.
Misalnya kita akan mengambil contoh dengan ukuran sampel n=2 yang diambil dari populasi tersebut. Peluang masing-masing satuan sampling untuk terpilih ke dalam sampel adalah sebesar 1/5. Sedangkan banyaknya kemungkinan sampel yang bisa dibentuk adalah sebanyak 10 atau dengan rumus N!/(n!x(N-n)!). Tapi ingat, kita hanya bekerja dengan satu sampel saja atau kita tidak mencoba semua kemungkinan sampel tersebut. Jika kita melakukan sensus terhadap populasi, artinya mengukur nilai X untuk semua anggota populasi sebanyak 5 buah, maka diperoleh nilai parameter μ (rata-rata X) sebesar 3 dengan σ2 (keragaman) sebesar …
Nilai kedua parameter tersebut dalan prakteknya tidak diketahui karena jika ukuran N sangat besarmaka sensus sulit dilakukan dengan pertimbangan waktu, biaya, atau tenaga. Tetapi melalui proses penelitian kita ingin menduga atau meyimpulkan parameter tersebut, yang dalam ilustrasi ini dengan mengambil 2 satuan sampling secara acak dari populasi tersebut. Berbagai nilai statistik untuk ke 10.
1. sampel yang mungkin dibentuk dapat dilihat pada Tabel berikut.
Sampel ke:
|
Satuan sampling Terpilih
|
Nilai X
|
X
|
Keragaman (s2)
|
1
|
A dan B
|
5 dan 4
|
4.5
|
0.5
|
2
|
A dan C
|
5 dan 3
|
4.0
|
2
|
3
|
A dan D
|
5 dan 2
|
3.5
|
4.5
|
4
|
A dan E
|
5 dan 1
|
3.0
|
8
|
5
|
B dan C
|
4 dan 3
|
3.5
|
0.5
|
6
|
B dan D
|
4 dan 2
|
3.0
|
2
|
7
|
B dan E
|
4 dan 1
|
2.5
|
4.5
|
8
|
C dan D
|
3 dan 2
|
2.5
|
0.5
|
9
|
C dan E
|
3 dan 1
|
2.0
|
2
|
10
|
D dan E
|
2 dan 1
|
1.5
|
0.5
|
Rata -rata
|
2.0
|
2.5
| ||
Dari tabel tersebut terlihat bahwa rata-rata X dari sebuah sampel yang diambil seorang peneliti mungkin lebih kecil, sama dengan atau lebih besar dari rata-rata populasi (μ =3). Artinya berdasarkan analisis statistik kita bisa menghitung seberapa besar tingkat kesalahan pendugaan parameter populasi untuk sampel tersebut. Untuk singkatnya, tingkat kesalahan tersebut disebut dengan standar error, yaitu dengan notasi dan rumus perhitungannya adalah sex = √[(N-n)/N)x(s2/n)], dan untuk populasi tak hingga atau persentase ukuran sampel terhadap ukuran populasi relatif sangat kecil rumus yang digunakan adalah sex = √(s2/n). Berdasarkan rumus standar error tersebut secaraumum bisa disimpulkan bahwa presisi penelitian bisa ditingkat (atau standar error semakin kecil) jika keragaman (heterogenitas populasi) semakin kecil dan atau ukuran sampel semakin besar.
4. Contoh soal 5-4
4. Contoh soal 5-4
Suatu populasi terdiri atas lima hasil pengukuran bernilai 2, 3, 6, 8, 11. Jika dari populasi ini hendak digunakan dua hasil pengukuran sebagai sampel, distribusi mean-mean sampling (sampling distribution of the means) yang bisa dibentuk jika sampling tanpa pergantian adalah…
Jawab
Kemungkinan sampel yang dibentuk adalah:
(2,3) (2,6) (2,8) (2,11) (3,6) (3,8) (3,11) (6,8) (6,11) (8,11)
Maka mean sampel yang terbentuk adalah:
2,5 4,0 5,0 6,5 4,5 5,5 7,0 8,5 9,5
Sehingga distribusi mean sampling dari sampel yang terbentuk adalah:
Mean sampel
|
2,5
|
4,0
|
5,0
|
6,5
|
4,5
|
5,5
|
7,0
|
8,5
|
9,5
|
Frekuensi
|
1
|
1
|
1
|
1
|
1
|
1
|
2
|
1
|
1
|
Probabilitas
|
1/10
|
1/10
|
1/10
|
1/10
|
1/10
|
1/10
|
1/10
|
1/10
|
1/10
|
Fungsi probabilitas dari suatu variabel acak X pada populasi ditunjukkan pada tabel berikut:
X
|
40
|
45
|
50
|
P (x)
|
0,2
|
0,3
|
0,5
|
Jika dilakukan sampling berukuran 2 dengan pergantian maka distribusi mean dan varians dari sampling dapat ditentukan sebagai berikut.
Kemungkinan sampel, probabilitas dan nilai serta s2 yang terbentuk adalah:
x1
|
x2
|
P(x1 dan x2)
|
s2
| |
40
|
40
|
(0,2) (0,2) = 0,04
|
40
|
0
|
40
|
45
|
(0,2) (0,3) = 0,06
|
42,5
|
12,5
|
40
|
50
|
(0,2) (0,5) = 0,10
|
45
|
50
|
45
|
40
|
(0,3) (0,2) = 0,06
|
42,5
|
12,5
|
45
|
45
|
(0,3) (0,3) = 0,09
|
45
|
0
|
45
|
50
|
(0,3) (0,3) = 0,15
|
47,5
|
12,5
|
50
|
40
|
(0,5) (0,2) = 0,10
|
45
|
50
|
50
|
45
|
(0,5) (0,3) = 0,15
|
47,5
|
12,5
|
50
|
50
|
(0,5) (0,5) = 0,25
|
50
|
0
|
40
|
42,5
|
45
|
47,5
|
50
| |
P(  ) |
0,04
|
0,12
|
0,29
|
0,30
|
0,25
|
Distribusi varians S2 dari sampling adalah:
s2
|
0
|
12,5
|
50
|
P (s2)
|
0,38
|
0,42
|
0,20
|
Jawab:
Untuk contoh-contoh tadi dapat dihitung rataannya masing-masing sehingga terbentuk sebaran peluang seperti tampak pada tabel berikut.
NO
|
CONTOH
|
RATAAN CONTOH
|
PELUANG MUNCULNYA CONTOH
|
1
|
{2 , 2}
|
2
|
1/16
|
2
|
{2 , 4}
|
3
|
1/16
|
3
|
{2 , 6}
|
4
|
1/16
|
4
|
{2 , 8}
|
5
|
1/16
|
5
|
{4 , 2}
|
3
|
1/16
|
6
|
{4 , 4}
|
4
|
1/16
|
7
|
{4 , 6}
|
5
|
1/16
|
8
|
{4 , 8}
|
6
|
1/16
|
9
|
{6 , 2}
|
4
|
1/16
|
10
|
{6 , 4}
|
5
|
1/16
|
11
|
{6 , 6}
|
6
|
1/16
|
12
|
{6 , 8}
|
7
|
1/16
|
13
|
{8 , 2}
|
5
|
1/16
|
14
|
{8 , 4}
|
6
|
1/16
|
15
|
{8 , 6}
|
7
|
1/16
|
16
|
{8 , 8}
|
8
|
1/16
|
Tabel Contoh Berukuran Dua yang Diambil Secara Acak Dengan Pemulihan
Dari sebaran sebelumnya kemudian dapat dibuat sebaran percontohan bagi rataan contoh, tampak pada Tabel berikut.
Tabel 5-2 Sebaran Rataan Contoh Dari Tabel 5-1
5.2. Dalil Limit Pusat
Dalam penggunaan dalil limit pusat, terdapat beberapa hal yang perlu diperhatikan antara lain:
a. Jumlah Sampel acak yang dapat ditarik dari suatu populasi sangat banyak.
Karenanya setiap statistik akan mempunyai variasi antar sampel.
Hal ini menjelaskan bahwa statistik-statistik tersebut berada dalam suatu distribusi atau sebaran.
b. Distribusi Sampling = Sebaran Penarikan Contoh
= sebaran peluang suatu statistik sampel
c. Statistik Sampel yang paling populer dipelajari adalah Mean
Dalam distribusi normal bisa digunakan dua kondisi:
Kondisi 1: n > 30, yaitu penaksiran dengan sampel besar (dasar teorema limit sentral)
Kondisi 2: n < 30, populasi berdistribusi normal, dan standar deviasi s diketahui (yaitu penaksiran dengan sampel kecil)
Selang penaksiran untuk mean populasi:
DISTRIBUSI SAMPLING BAGI MEAN
Beberapa notasi:
DALIL LIMIT PUSAT = THE CENTRAL LIMIT THEOREM
Dalil Limit Pusat berlaku untuk contoh yang diambil dari populasi besar, selama populasi berukuran besar, distribusi populasi tidak dipersoalkan.
Contoh :
Populasi : berukuran N besar
berukuran = n diambil dari distribusi sembarang
MAKA
sebaran untuk nilai rata-rata akan mendekati distribusi normal dengan:
· Dalil Limit Pusat untuk : - penarikan sampel dari populasi yang sangat besar
- distribusi populasi tidak dipersoalkan
· Beberapa buku mencatat hal berikut : Populasi dianggap BESAR jika ukuran sampel
KURANG DARI 5 % ukuran populasi atau
Contoh 1:
PT AKUA sebuah perusahaan air mineral rata-rata setiap hari memproduksi 100 juta gelas air mineral. Perusahaan ini menyatakan bahwa rata-rata isi segelas AKUA adalah 250 ml dengan standar deviasi = 15 ml. Rata-rata populasi dianggap menyebar normal.
Jika sampel diperkecil menjadi 25 gelas, hitunglah :
a. standard error atau galat baku sampel tersebut?
b. peluang rata-rata sampel akan berisi lebih dari 255 ml?
Diselesaikan dengan DALIL LIMIT PUSAT ® karena POPULASI SANGAT BESAR
Contoh 2:
Dari populasi 800 pekerja diambil sample dengan n=50. Dari sampel tersebut diketahui bahwa mean pendapatan per minggu =$245,60 dengan standar deviasi s=$ 26,45. Tidak ada informasi apakah populasinya berdistribusi normal atau tidak. Jika kita menggunakan 95% derajat keyakinan (artinya kita yakin bahwa dalam penyampelan berulang, 95% dari mean sampel akan mewakili mean populasi m). Tentukan selang atau interval untuk menaksir mean populasi.
Jawab:
Tahap 1
Populasinya tidak diketahui apakah berdistribusi normal atau tidak, tetapi karena kita menggunakan sampel besar (n=50, sehingga lebih dari 30), maka kita diperbolehkan menggunakan distribusi normal.
Tahap 2
Tahap 3
Derajat keyakinan yang digunakan adalah 95% atau 0,95. Kita memakai setengah dari nilai z yaitu 0,475 untuk nilai probabilitas maka nilai z = ± 1,96 (lihat tabel).
Tahap 4
Sekarang kita bisa masukan rumus selang penaksiran selengkapnya:
Jadi, dengan derajat keyakinan 95% dalam jangka panjang selang antara $238,50 sampai dengan $252,70 akan berisi mean pendapatan rumah tangga populasi.
Contoh 3:
Dengan informasi pada contoh 2, buatlah selang mean populasi dengan derajat keyakinan 90%.
Jawab:
Karena yang berubah hanyalah derajat keyakinannya, maka yang perlu diubah hanyalah nilai z. Dengan 90% derajat keyakinan maka probabilitasnya setengah adalah 0,45. Untuk nilai probabilitas 0,45 nilai z adalah 1,65, sehingga selang penaksirannya akan menjadi:
Jadi, dengan derajat keyakinan 90% dalam jangka panjang selang antara $239,63 sampai dengan $251,57 akan berisi mean pendapatan rumah tangga populasi.
5.3. Sebaran t-student
Distribusi t adalah distribusi yang mirip dengan distribusi normal, dengan beberapa perbedaan. Berikut ini beberapa ciri tentang distribusi t:
a. Mean distribusi (yang bernilai 0) terletak ditengah dan membagi daerah menjadi dua dengan luas yang sama (sifat simetris).
b. Skala yang digunakan adalah skala t.
c. Terdapat berbagai bentuk distribusi tergantung dari derajat bebasnya. Derajat bebas dilambangkan dengan df (degree of freedom) besarnya = n – 1 dimana n adalah jumlah anggota dalam sampel semakin besar derajat bebasnya, maka distribusi t akan semakin mendekati distribusi normal.
d. Jika kita mengetahui nilai probabilitas (dari derajat keyakinannya) dan derajat bebasnya, maka kita bisa mencari nilai t nyadengan melihat tabel t yang telah dibuat oleh para ahli statistik.
Perhatikan perbandingan distribusi t dan distribusi normal dalam gambar di atas.
Carilah t untuk derajat keyakinan 95% dan derajat bebas 15. Untuk mencari nilai t, perlu dipahami terlebih dahulu konsep derajat kesalahn, atau tingkat kesalahan yang ditolerir atau tingkat kesalahan yang dimaafkan yang dilambangkan dengan a yang besarnya adalah 1 – derajat keyakinan. Untuk contoh di atas, derajat keyakinan adalah 95% sehingga a = 1 – 0,95 = 0,05. Karena kiri-kanan sama, maka yang kita gunakan hanyalah ½a = ½ (0,05) = 0,025. Letak dari nilai ½a akan berada di tabel bagian paling atas. Bagian paling kiri tabel berisi derajat bebasnya. Maka untuk derajat keyakinan (dk) = 95% dan df = 15, nilai t adalah 2,131 (periksa tabel t).
Seperti distribusi normal, distribusi t juga bisa digunakan untuk menaksir mean populasi dengan menggunakan mean sampel. Untuk menggunakan distribusi t ini diperlukan situasi khusus, yaitu situasi dengan syarat-syarat sebagai berikut:
a. Ukuran sampelnya kecil (n < 30)
b. Distribusi populasinya adalah distribusi normal
c. Standar deviasi populasi s tidak diketahui (yang diketahui adalah standar deviasi sampel s)
Ketiga syarat tersebut harus dipenuhi secara bersama-sama. Rumus selang penaksiran mean populasi dengan distribusi t akan menjadi sebagai berikut:
Contoh 4:
Dari sebuah pabrik batu baterai yang diasumsikan berdistribusi normal diambil 9 buah baterai sebagai sampel dan diukur daya tahan batu baterai tersebut. Setelah diteliti, ternyata mean daya tahan batu baterai tersebut = 20 jam dengan standar deviasi s = 3 jam. Tentukan selang penaksiran rata-rata daya tahan batu baterai populasi untuk derajat keyakinan 95%.
Dari sebuah pabrik batu baterai yang diasumsikan berdistribusi normal diambil 9 buah baterai sebagai sampel dan diukur daya tahan batu baterai tersebut. Setelah diteliti, ternyata mean daya tahan batu baterai tersebut = 20 jam dengan standar deviasi s = 3 jam. Tentukan selang penaksiran rata-rata daya tahan batu baterai populasi untuk derajat keyakinan 95%.
Jawab:
Karena n = 9 (sampel kecil), distribusi populasinya distribusi normal, dan yang diketahui adalah deviasi standar sampel s, maka rumus penaksiran yang teapat adalah dengan ditribusi t.
Angka-angka yang diperlukan:
Angka-angka yang diperlukan:
Nilai t, diperoleh dari informasi df = n – 1 = 9 – 1 = 8
Dan tingkat signifikansi a = 1 – 0,95 = 0,05, sehingga ½ a = 0,025.
Nilai t8, dengan ½ a = 0,025 adalah ± 2,306.
Jadi, dengan 95% derajat keyakinan, selang antara 17,7 jam sampai dengan 22,3 jam akan berisi mean daya tahan batu baterai yang sebenarnya.
Contoh 5:
Untuk kasus pada contoh 4 di atas, carilah selang penaksiran mean populasi dengan derajat keyakinan 90%.
Jawab:
Yang harus kita lakukan hanyalah mengubah nilai t. Untuk derajat keyakinan 90%, berarti a = 0,10 sehingga ½ a = 0,05 adalah ± 1,860. Maka rumus di atas akan menjadi:
Jadi, dengan 90% derajat keyakinan, selang antara 18,14 jam sampai dengan 21,86 jam akan berisi mean daya tahan batu baterai yang sebenarnya.
 |
| tabel nilai z |
 |
| tabel distribusi t |
_________________________
Daftar Pustaka
Hamang, Abdul. 2005. Metode Statistika. Jakarta: Graha Ilmu
Hakim, Abdul. 2002. Statistik Induktif untuk Ekonomi dan Bisnis. Yogyakarta: Ekonisia
Saefudin, Asep. 2009. Statistika Dasar. Bogor: Grasindo
Usman, Husain dan Purnomo Schady. 2006. Pengantar Statistika. Jakarta: Bumi Aksara
