Pebuah Acak ( I )

SUB TOPIK

4.1 Definisi Peubah Acak

4.2 Sebaran Peubah Acak

4.3 Nilai Harapan dan Ragam Peubah Acak

URAIAN MATERI

Nilai-nilai peubah yang dicatat dalam suatu contoh acak adalah nilai-nilai dari titik-titik contoh yang masuk ke dalam suatu contoh. Nilai peubah ini adalah realisasi dari peluang, dan mengekspresikan suatu kejadian acak. Peubah demikian, yang nilai-nilainya muncul menurut peluangnya masing-masing dinamakan sebagai peubah acak (random variable).

4.1 Definisi Peubah Acak

Peubah Acak adalah suatu fungsi yang memetakan setiap elemen dalam ruang sampel dengan tepat satu bilangan real. Peubah acak merepresentasikan setiap hasil eksperimen/ pengukuran dengan suatu nilai real.

Saat dilakukan pengundian sekeping uang logam, bila focus perhatian hanya pada berapa kali sisi gambar muncul, maka nilai numeric 0,1,2 atau 3 dapat muncul pada setiap titik sampel. Bilangan ini merupakan besaran acak yang nilainya ditentukan oleh hasil percobaan. Nilai-nilai ini dipandang sebagai nilai-nilai yang dapat diambil oleh suatu peubah acak atau variabel acak X, yang dalam hal ini menyatakan berapa kali sisi gambar muncul bila sekeping uang logam dilempar sebanyak 3 kali.

Huruf kapital, misal X, untuk melambangkan suatu peubah acak, dan huruf kecilnya, misalkan x, untuk menyatakan salah satu di antara nilai-nilainya.

Misalkan dalam pengetosan sebuah dadu 1 kali, ruang sampel adalah {S1, S2, S3, S4, S5, S6}. Diberikan pernyataan yang berbunyi: ”muncul sisi genap dari dadu tersebut”. Dengan adanya statement ini, kita akan berpikir bisa muncul bisa juga tidak. Jika kita misalkan untuk muncul sisi genap 1, dan tidak muncul sisi genap 0, maka bisa kita dapat gambarkan pemetaannya sebagai berikut:

 Contoh lain:

Dua buah uang logam ditos satu kali, kemudian diberikan pernyataan banyaknya sisi angka yang muncul. Dari percobaan di atas maka ruang sampel {(AA), (AG), (GA), (GG)}.Jika ada statement di atas maka kita akan berpikir bisa tidak muncul ( 0 ), bisa muncul 1 bisa muncul 2. Jika dinyatakan dalam suatu dalam pemetaan maka bisa digambarkan sbb:

Perhatikan bahwa peubah acak adalah pemaknaan numerik atas kejadian-kejadian dalam ruang contoh. Dalam bentuk numerik ini, analisis terhadap kejadian-kejadian yang mungkin muncul dari suatu tindakan berpeluang selanjutnya dapat dibuat berdasar kaidah-kaidah yang berlaku pada himpunan bilangan nyata.

4.2 Sebaran Peubah Acak

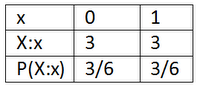
Masing-masing peubah acak memiliki peluang yang besarnya bergantung dengan kejadian yang menghasilkannya. Pada pelemparan koin, peluang X bernilai 0 dan peluang X bernilai 1 masing-masing adalah .

Peubah acak dilambangkan oleh huruf besar misalnya X sedangkan nilai nilai real dalam pebuah acak  dilambangkan oleh x. Yang dimaksud sebaran peubah acak adalah banyaknya titik sampel yang berpasangan dengan nilai real peubah acak yang dimaksud. Atau dengan kata lain berapa banyak dari nilai real peubah acak menyebar di dalam ruang sampel.

Terlihat pada contoh pertama tampak bahwa nilai real peubah acak adalah 0 dan 1. Tampak bahwa ada tiga titik sampel yang berpasangan dengan 0 dan tiga titik sampel yang berpasangan dengan 1.

Untuk contoh kedua tampak bahwa nilai real peubah acak adalah 0,1 dan 2. Tampak ada satu titik sampel berpasangan dengan 0, dua titik sampel berpasangan dengan 1 dan satu titik sampel berpasangan 2. Sehingga jika dinyatakan dalam tabel adalah sebagai berikut:

Contoh 1                                                                               Contoh 2

Selanjutnya yang dimaksud sebaran peubah acak adalah peluang dari masing-masing sebaran. Definisi peluang adalah perbandingan antara titik sampel dan ruang sampel, sehingga tabel di atas dapat ditentukan sebaran peluang peubah sampel sebagai berikut:

Contoh 1 Contoh 2

Tabel peubah acak pemunculan minimal 1 angka pada lemparan 2 koin (contoh 2).

Sebaran Peubah Acak pemunculan 1 angka pada pelemparan 2 koin.

Fungsi Peluang

Peubah pengukuran (kuantitatif), yaitu peubah yang dihasilkan melalui proses pengukuran dengan menggunakan alat ukur tertentu menghasilkan peubah acak kontinu. Hasil yang mungkin keluar adalah sebuah gugus bilangan nyata yang kontinu dan sangat rapat.

Untuk peubah kontinu, fungsi peluang, y = f(x) , menyatakan sebaran peluang peubah pengukuran, yang secara visual ditampilkan dalam bentuk kurva sebaran. Sebagai suatu sebaran peluang, fungsi peluang mempunyai sifat-sifat:

1.      Jumlah nilai fungsi selang peubah tertentu minimal 0 dan maksimal 1

2.      Jumlah nilai fungsi seluruh wilayah X adalah 1

3.      Jumlah nilai fungsi seluruh wilayah di luar X adalah 0

Sebaran Fungsi Peluang

4.3 Nilai Harapan dan Ragam Peubah Acak

Distribusi probabilitas memiliki berbagai sifat atau karakteristik yang dapat digunakan untuk mengidentifikasi suatu distribusi. Karakteristik yang biasa digunakan antara lain rata-rata hitung yang biasa disebut “harapan matematis” (atau nilai harapan) dan ragam peubah acak. Nilai harapan dari peubah acak adalah pemusatan dari nilai peubah acak jika percobaannya dilakukan secara berulang-ulang sampai tak berhingga kali.

Nilai harapan peubah acak diskrit X, dilambangkan dengan E(X), didefinisikan sebagai jumlah hasil kali peubah acak dengan masing-masing peluangnya. Nilai harapan fungsi peluang kontinu X adalah jumlah hasil kali x dengan f(x), pada semua selang peubah acak yang terdefinisi untuk X,

Nilai harapan suatu peubah acak adalah pusat peubah acak sering pula dinamakan nilai-tengah populasi, dilambangkan dengan µ.

Nilai harapan kuadrat simpangan peubah acak ( X - µ)² adalah jumlah hasil kali kuadrat simpangan peubah acak dari µ dengan masing-masing peluangnya, atau jumlah hasil kali (X-µ)² dengan f(x), pada semua selang peubah acak. Nilai harapan kuadrat simpangan peubah acak tersebut menunjukkan ragam peubah acak tersebut

Sifat-sifat nilai harapan:

1. Jika c konstanta maka E(c ) = c
2. Jika peubah acak X dikalikan dengan konstanta c maka E(cX) = c E(X)
3. Jika X dan Y peubah acak maka E(XY)  =  E(X) E(Y)

CONTOH SOAL

1.      Dua bola diambil berturutan secara acak, tanpa penggantian, dari suatu wadah yang berisi empat bola merah (R) dan tiga bola hitam (B). Hasil dapat muncul dan nilai y dari peubah acak Y, dimana Y menyatakan banyaknya bola merah adalah

2.      Petugas penyimpanan helm mengembalikan helm dari tiga orang mahasiswa; Sandy, Jamet, dan Bagus dalam urutan sepert itu. Jika helm diambil acak dan dikembalikan sesuai urutan pegawai diatas, dan m menyatakan jumlah helm yang kembali ke pemilik sebenarnya , kemungkinan berikut bisa terjadi: