10.5 Calculation of moment inertia
Moment of inertia of a rigid object is :
I= ʃ r2dm
Parallel-axis theorem
“Suppose the of inertia about an axis through the center of mass of an object is The parallel-axis theorem states that the moment of inertia about any axis parallel to and a distance D away from this axis is: ICM +MD2
10.6 Torque
where d is the moment arm of the force, which is the perpendicular distance from therotation axis to the line of action of the force. Torque is a measure of the tendency of
the force to change the rotation of the object about some axis.
When a force is exerted on a rigid object pivoted about an axis, the object tends to rotate about that axis. The tendency of a force to rotate an object about some axis is measured by a vector quantity called torque τ (Greek tau). Torque is a vector, but we
will consider only its magnitude here and explore its vector nature in Chapter 11.
Consider the wrench pivoted on the axis through O in Figure 10.13. The applied
force F acts at an angle ϕ to the horizontal. We define the magnitude of the torque associate
with the force F by the expression :
10.7 Relationship Between Torque and Angular Acceleration.
In Chapter 4, we learned that a net force on an object causes an acceleration of the object and that the acceleration is proportional to the net force (Newton’s second law). In this section we show the rotational analog of Newton’s second law—the angular acceleration of a rigid object rotating about a fixed axis is proportional to the net torque acting about that axis. Before discussing the more complex case of rigid-object rotation, however, it is instructive first to discuss the case of a particle moving in a circular path about some fixed point under the influence of an external force.
Consider a particle of mass m rotating in a circle of radius r under the influence of a tangential force Ft and a radial force Fr , as shown in Figure 10.16. The tangential force provides a tangential acceleration at, and
The magnitude of the torque about the center of the circle due to Ft is
Because the tangential acceleration is related to the angular acceleration through the relationship at " r( (see Eq. 10.11), the torque can be expressed as Recall, the torque can be expressed as
That is, the torque acting on the particle is proportional to its angular acceleration, and the proportionality constant is the moment of inertia. Note that τ = I α is the rotational analog of Newton’s second law of motion, F = ma.
Now let us extend this discussion to a rigid object of arbitrary shape rotating about a fixed axis, as in Figure 10.17. The object can be regarded as an infinite number of mass elements dm of infinitesimal size. If we impose a Cartesian coordinate system on the object, then each mass element rotates in a circle about the origin, and each has a tangential acceleration at produced by an external tangential force dFt . For any given element, we know from Newton’s second law that
The torque dτ associated with the force dFt acts about the origin and is given by
Because αt = rα the expression for dτ becomes
Although each mass element of the rigid object may have a different linear acceleration at , they all have the same angular acceleration With this in mind, we can integrate the above expression to obtain the net torque ∑τ about O due to the external forces:
where ( can be taken outside the integral because it is common to all mass elements. From Equation 10.17, we know that ʃ r2 dm is the moment of inertia of the object about the rotation axis through O, and so the expression for ∑τ becomes
Note that this is the same relationship we found for a particle moving in a circular path (see Eq. 10.20). So, again we see that the net torque about the rotation axis is proportional to the angular acceleration of the object, with the proportionality factor being I, a quantity that depends upon the axis of rotation and upon the size and shape of the object. In view of the complex nature of the system, the relationship ∑τ = Iα is strikingly simple and in complete agreement with experimental observations.
Finally, note that the result ∑τ = Iα also applies when the forces acting on the mass elements have radial components as well as tangential components. This is because the line of action of all radial components must pass through the axis of rotation, and hence all radial components produce zero torque about that axis.
10.8 work, Power, and Energy in Rotational Motion
Up to this point in our discussion of rotational motion in this chapter, we focused on an approach involving force, leading to a description of torque on a rigid object. We now see how an energy approach can be useful to us in solving rotational problems.
We begin by considering the relationship between the torque acting on a rigid object and its resulting rotational motion in order to generate expressions for power and a rotational analog to the work–kinetic energy theorem. Consider the rigid object pivoted at O in Figure 10.22. Suppose a single external force F is applied at P, where F lies in the plane of the page. The work done by F on the object as it rotates through an infinitesimal
Distance ds = rdθ is 
where F sin 3 is the tangential component of F, or, in other words, the component of
the force along the displacement. Note that the radial component of F does no work because
it is perpendicular to the displacement.
Because the magnitude of the torque due to F about O is defined as rF sin θ by Equation 10.19, we can write the work done for the infinitesimal rotation as
The rate at which work is being done by F as the object rotates about the fixed axis through the angle dθ in a time interval dt is
Because dW/dt is the instantaneous power (see Section 7.8) delivered by the forceand d!/dt " &, this expression reduces to
This expression is analogous to P= Fv in the case of linear motion, and the expression dW = τdθ is analogous to dW = Fx dx.
In studying linear motion, we found the energy approach extremely useful in describing the motion of a system. From what we learned of linear motion, we expect that when a symmetric object rotates about a fixed axis, the work done by external forces equals the change in the rotational energy.
To show that this is in fact the case, let us begin with ∑τ = Iα Using the chain rule from calculus, we can express the resultant torque as
Rearranging this expression and noting that ∑τdθ = dW , we obtain
Integrating this expression, we obtain for the total work done by the net external force acting on a rotating system
where the angular speed changes from &i to &f . That is, the work–kinetic energy theorem for rotational motion states that
“the net work done by external forces in rotating a symmetric rigid object about a fixed axis equals the change in the object’s rotational energy”
In general, then, combining this with the translational form of the work–kinetic energy theorem from Chapter 7, the net work done by external forces on an object is the change in its total kinetic energy, which is the sum of the translational and rotational kinetic energies. For example, when a pitcher throws a baseball, the work done by the pitcher’s hands appears as kinetic energy associated with the ball moving through space as well as rotational kinetic energy associated with the spinning of the ball.
In addition to the work–kinetic energy theorem, other energy principles can also be applied to rotational situations. For example, if a system involving rotating objects is isolated, the principle of conservation of energy can be used to analyze the system.
Table 10.3 lists the various equations we have discussed pertaining to rotational motion, together with the analogous expressions for linear motion. The last two equations in Table 10.3, involving angular momentum L, are discussed in Chapter 11 and are included here only for the sake of completeness.
10.9 Rolling Motion of a Rigid Object
In this section we treat the motion of a rigid object rolling along a flat surface. Ingeneral, such motion is very complex. Suppose, for example, that a cylinder is rolling on a straight path such that the axis of rotation remains parallel to its initial orientation in space. As Figure 10.26 shows, a point on the rim of the cylinder moves in a complex path called a cycloid. However, we can simplify matters by focusing on the center of mass rather than on a point on the rim of the rolling object. As we see in Figure 10.26, the center of mass moves in a straight line. If an object such as a cylinder rolls without slipping on the surface (we call this pure rolling motion), we can show that a simple relationship exists between its rotational and translational motions.
Consider a uniform cylinder of radius R rolling without slipping on a horizontal surface (Fig. 10.27). As the cylinder rotates through an angle !, its center of mass moves a linear distance s = Rθ (See Eq. 10.1a). Therefore, the linear speed of the center of mass for pure rolling motion is given by
Where & is the angular speed of the cylinder. Equation 10.25 holds whenever a cylinder or sphere rolls without slipping and is the condition for pure rolling motion
The magnitude of the linear acceleration of the center of mass for pure rolling motion is
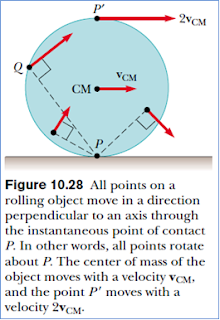The linear velocities of the center of mass and of various points on and within the cylinder are illustrated in Figure 10.28. A short time after the moment shown in the drawing, the rim point labeled P might rotate from the six o’clock position to, say, the seven o’clock position, while the point Q would rotate from the ten o’clock position to the eleven o’clock position, and so on. Note that the linear velocity of any point is in a direction perpendicular to the line from that point to the contact point P. At any instant, the part of the rim that is at point P is at rest relative to the surface because slipping does not occur. All points on the cylinder have the same angular speed. Therefore, because the distance from P1 to P is twice the distance from P to the center of mass, P1 has a speed 2vCM = 2ω. To see why this is so, let us model the rolling motion of the cylinder in Figure 10.29 as a combination of translational (linear) motion and rotational motion. For the pure translational motion shown in Figure 10.29a, imagine that the cylinder does not rotate, so that each point on it moves to the right with speed vCM. For the pure rotational motion shown in Figure 10.29b, imagine that a rotation axis through the center of mass is stationary, so that each point on the cylinder has the same angular speed &. The combination of these two motions represents the rolling motion shown in Figure 10.29c. Note in Figure 10.29c that the top of the cylinder has linear speed vCM + Rω + vCM + vCM = 2vCM, which is greater than the linear speed of any other point on the cylinder. As mentioned earlier, the center of mass moves with linear speed vCM while the contact point between the surface and cylinder has a linear speed of zero.
We can express the total kinetic energy of the rolling cylinder as
Where IP is the moment of inertia about a rotation axis through P. Applying the parallel-axis theorem, we can substitute IP =ICM + MR2 into Equation 10.27 to obtain
The term 1/2ICMω2 represents the rotational kinetic energy of the cylinder about its center of mass, and the term ½ Mv CM2 represents the kinetic energy the cylinder would have if it were just translating through space without rotating. Thus, we can say that the total kinetic energy of a rolling object is the sum of the rotational kinetic energy about the center of mass and the translational kinetic energy of the center of mass.
For the system of the sphere and the Earth, we define the zero configuration of gravitational potential energy to be when the sphere is at the bottom of the incline. Thus, conservation of mechanical energy gives us
Tidak ada komentar:
Posting Komentar