The central topic of this chapter is angular momentum, a quantity that plays a key role in rotational dynamics. In analogy to the principle of conservation of linear momentum, we find that the angular momentum of a system is conserved if no external torques act on the system. Like the law of conservation of linear momentum, the law of conservation of angular momentum is a fundamental law of physics, equally valid for relativistic and quantum systems.
1. The Vector Product and Torque
An important consideration in defining angular momentum is the process of multiplying two vectors by means of the operation called the vector product. We will introduce the vector product by considering torque as introduced in the preceding chapter.
Consider a force F acting on a rigid object at the vector position r (Fig. 11.1). As we saw in Section 10.6, the magnitude of the torque due to this force relative to the origin is r F sin Ѳ, where Ѳ is the angle between r and F. The axis about which F tends to produce rotation is perpendicular to the plane formed by r and F.
The torque vector τ is related to the two vectors r and F. We can establish a mathematical relationship between τ , r, and F using a mathematical operation called the vector product, or cross product :
We now give a formal definition of the vector product. Given any two vectors A and B, the vector product A X B is defined as a third vector C, which has a magnitude of AB sin ѳ, where ѳ is the angle between A and B. That is, if C is given by :
Then its magnitude is
The quantity AB sin Ѳ is equal to the area of the parallelogram formed by A and B, as shown in Figure 11.2. The direction of C is perpendicular to the plane formed by A and B, and the best way to determine this direction is to use the right-hand rule illustrated in Figure 11.2. The four fingers of the right hand are pointed along A and then “wrapped” into B through the angle Ѳ. The direction of the upright thumb is the direction of A X B = C. Because of the notation, A x B is often read “A cross B”; hence, the term cross product.
Some properties of the vector product that follow from its definition are as follows:
1. Unlike the scalar product, the vector product is not commutative. Instead, the order in which the two vectors are multiplied in a cross product is important :
Therefore, if you change the order of the vectors in a cross product, you must change the sign. You can easily verify this relationship with the right-hand rule.
2. If A is parallel to B (Ѳ = 0° or 180°), then A x B = 0; therefore, it follows that A x A = 0.
3. If A is perpendicular to B, then |A x B| = AB.
4. The vector product obeys the distributive law :
5. The derivative of the cross product with respect to some variable such as t is
where it is important to preserve the multiplicative order of A and B,
1. Angular Momentum
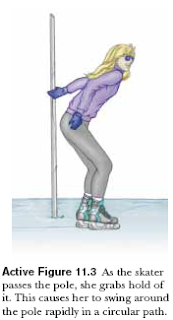 Imagine a rigid pole sticking up through the ice on a frozen pond (Fig. 11.3). A skater glides rapidly toward the pole, aiming a little to the side so that she does not hit it. As she approaches the pole, she reaches out and grabs it, an action that causes her to move in a circular path around the pole. Just as the idea of linear momentum helps us analyze translational motion, a rotational analog—angular momentum—helps us analyze the motion of this skater and other objects undergoing rotational motion. Consider a particle of mass m located at the vector position r and moving with linear momentum p as in Figure 11.4. In describing linear motion, we found that the net force on the particle equals the time rate of change of its linear momentum, ΣF = dp/dt (see Eq. 9.3). Let us take the cross product of each side with r, which gives us the net torque on the particle on the left side of the equation :
Imagine a rigid pole sticking up through the ice on a frozen pond (Fig. 11.3). A skater glides rapidly toward the pole, aiming a little to the side so that she does not hit it. As she approaches the pole, she reaches out and grabs it, an action that causes her to move in a circular path around the pole. Just as the idea of linear momentum helps us analyze translational motion, a rotational analog—angular momentum—helps us analyze the motion of this skater and other objects undergoing rotational motion. Consider a particle of mass m located at the vector position r and moving with linear momentum p as in Figure 11.4. In describing linear motion, we found that the net force on the particle equals the time rate of change of its linear momentum, ΣF = dp/dt (see Eq. 9.3). Let us take the cross product of each side with r, which gives us the net torque on the particle on the left side of the equation :Now let us add to the right-hand side the term dr/dt x p which is zero because dr/dt = v and v and p are parallel.
We recognize the right-hand side of this equation as the derivative of r x p
This looks very similar in form to ΣF= dp/dt This suggests that the combination r " p should play the same role in rotational motion that p plays in translational motion. We call this combination the angular momentum of the particle:
This allows us to write
which is the rotational analog of Newton’s second law, ΣF = dp/dt. Note that torque causes the angular momentum L to change just as force causes linear momentum p to change. Equation Στ = dL/dt states that the torque acting on a particle is equal to the time rate of change of the particle’s angular momentum.
Note that Στ = dL/dt is valid only if Στ and L are measured about the same origin. (Of course, the same origin must be used in calculating all of the torques.) Furthermore, the expression is valid for any origin fixed in an inertial frame.
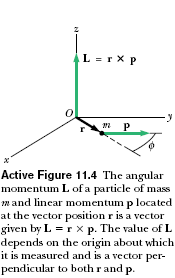 The SI unit of angular momentum is kg ·m2/s. Note also that both the magnitude and the direction of L depend on the choice of origin. Following the right-hand rule, we see that the direction of L is perpendicular to the plane formed by r and p. In Figure 11.4, r and p are in the xy plane, and so L points in the z direction. Because p = mv, the magnitude of L is
The SI unit of angular momentum is kg ·m2/s. Note also that both the magnitude and the direction of L depend on the choice of origin. Following the right-hand rule, we see that the direction of L is perpendicular to the plane formed by r and p. In Figure 11.4, r and p are in the xy plane, and so L points in the z direction. Because p = mv, the magnitude of L isL = mvr sin Ф
where Ф is the angle between r and p. It follows that L is zero when r is parallel to p (Ф = 0 or 180°). In other words, when the linear velocity of the particle is along a line that passes through the origin, the particle has zero angular momentum with respect to the origin. On the other hand, if r is perpendicular to p ( Ф = 90°), then L = mvr. At that instant, the particle moves exactly as if it were on the rim of a wheel rotating about the origin in a plane defined by r and p.
Angular Momentum of a System of Particles
This equation states that the net external force on a system of particles is equal to the time rate of change of the total linear momentum of the system. Let us see if there is a similar statement that can be made in rotational motion. The total angular momentum of a system of particles about some point is defined as the vector sum of the angular momenta of the individual particles
where the vector sum is over all n particles in the system
Let us differentiate this equation with respect to time:
The torques acting on the particles of the system are those associated with internal forces between particles and those associated with external forces. However, the net torque associated with all internal forces is zero. To understand this, recall that Newton’s third law tells us that internal forces between particles of the system are equal in magnitude and opposite in direction. If we assume that these forces lie along the line of separation of each pair of particles, then the total torque around some axis passing through an origin O due to each action–reaction force pair is zero. That is, the moment arm d from O to the line of action of the forces is equal for both particles and the forces are in opposite directions. In the summation, therefore, we see that the net internal torque vanishes. We conclude that the total angular momentum of a system can vary with time only if a net external torque is acting on the system, so that we have
That is :
Although we do not prove it here, the following statement is an important theorem concerning the angular momentum of a system relative to the system’s center of mass :
This theorem applies even if the center of mass is accelerating, provided τ and L are evaluated relative to the center of mass.
1. Angular Momentum of a Rotating Rigid Object
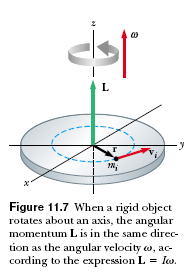 we considered the angular momentum of a deformable system. Let us now restrict our attention to a nondeformable system—a rigid object. Consider a rigid object rotating about a fixed axis that coincides with the z axis of a coordinate system, as shown in Figure 11.7. Let us determine the angular momentum of this object. Each particle of the object rotates in the xy plane about the z axis with an angular speed ω
we considered the angular momentum of a deformable system. Let us now restrict our attention to a nondeformable system—a rigid object. Consider a rigid object rotating about a fixed axis that coincides with the z axis of a coordinate system, as shown in Figure 11.7. Let us determine the angular momentum of this object. Each particle of the object rotates in the xy plane about the z axis with an angular speed ωThe magnitude of the angular momentum of a particle of mass mi about the z axis is miviri. Because vi = riω , we can express the magnitude of the angular momentum of this particle as
The vector Li is directed along the z axis, as is the vector ω. We can now find the angular momentum (which in this situation has only a z component) of the whole object by taking the sum of Li over all particles:
where we have recognized Σmiri as the moment of inertia I of the object about the z axis with respect to time, noting that I is constant for a rigid object:
where α is the angular acceleration relative to the axis of rotation. Because dLz /dt is equal to the net external torque
That is, the net external torque acting on a rigid object rotating about a fixed axis equals the moment of inertia about the rotation axis multiplied by the object’s angular acceleration relative to that axis. This equation is also valid for a rigid object rotating about a moving axis provided the moving axis (1) passes through the center of mass and (2) is a symmetry axis.
If a symmetrical object rotates about a fixed axis passing through its center of mass, in vector form as L = Iω, where L is the total angular momentum of the object measured with respect to the axis of rotation. Furthermore, the expression is valid for any object, regardless of its symmetry, if L stands for the component of angular momentum along the axis of rotation.



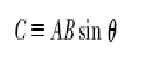





















Tidak ada komentar:
Posting Komentar