6.1 Newton’s Second Law Applied to Uniform Circular
Motion
Motion
A particle moving with uniform speed v in a circular path of radius r experiences an acceleration that has a magnitude.
The acceleration is called centripetal acceleration because ac is directed toward the center of the circle. Furthermore, ac is always perpendicular to v. (If there were a component of acceleration parallel to v, the particle’s speed would be changing.)
Consider a ball of mass m that is tied to a string of length r and is being whirled at constant speed in a horizontal circular path, as illustrated in Figure 6.1. Its weight is supported by a frictionless table. Why does the ball move in a circle? According to Newton’s first law, the ball tends to move in a straight line; however, the string prevents
Motion along a straight line by exerting on the ball a radial force Fr that makes it follow the circular path. This force is directed along the string toward the center of the circle, as shown in Figure 6.1. If we apply Newton’s second law along the radial direction, we find that the net force causing the centripetal acceleration can be evaluated:
A force causing a centripetal acceleration acts toward the center of the circular path and causes a change in the direction of the velocity vector. If that force should vanish, the object would no longer move in its circular path; instead, it would move along a straight-line path tangent to the circle. This idea is illustrated in Figure 6.2 for the ball whirling at the end of a string in a horizontal plane. If the string breaks at some instant, the ball moves along the straight-line path tangent to the circle at the point where the string breaks.
6.2 Nonuniform Circular Motion
We found that if a particle moves with varying speed in a circular path,there is in addition to the radial component having magnitude dv/dt Therefore,the force acting on the particle must also have a tangential and a radial component. Because the total acceleration is a = at + av ( at, the total force exerted on the particle is , ∑F = ∑Fr + ∑Fv as shown in, Figure 6.8. The vector ∑Fr is directed toward the center of the circle and is responsible for the centripetal acceleration. The vector ∑Fv tangent to the circle is responsible for the tangential acceleration, which represents a change in the speed of the particle with time.
6.3 Motion in Accelerated Frames
In this section, we analyze how Newton’s second law is applied by an obserbver in a non inertial frame of reference, that is, on that is accelerating.
Another fictitious force is due to the change in the direction of the velocity vector.
To understand the motion of a system that is noninertial because of a change in direction,
consider a car traveling along a highway at a high speed and approaching a curved exit ramp, as shown in Figure 6.11a. As the car takes the sharp left turn onto the
ramp, a person sitting in the passenger seat slides to the right and hits the door. At that
point, the force exerted by the door on the passenger keeps her from being ejected from
the car. What causes her to move toward the door? A popular but incorrect explanation
is that a force acting toward the right in Figure 6.11b pushes her outward. This is often
called the “centrifugal force,” but it is a fictitious force due to the acceleration associated
with the changing direction of the car’s velocity vector. (The driver also experiences this
effect but wisely holds on to the steering wheel to keep from sliding to the right.)
Another fictitious force is the “Coriolis force.” This is an apparent force
caused by changing the radial position of an object in a rotating coordinate system. For
example, suppose you and a friend are on opposite sides of a rotating circular platform
and you decide to throw a baseball to your friend. As Figure 6.12a shows, at t = 0 you
throw the ball toward your friend, but by the time tf when the ball has crossed the platform,
your friend has moved to a new position.
Fictitious forces may not be real forces, but they can have real effects.
Motion in the Presence of Resistive Forces
The magnitude of the resistive force can depend on speed in a complex way, and
here we consider only two situations
In the first situation, Resistive Force Proportional to Object Speed.
this assumption is valid for objects falling slowly through a liquid and for very small objects, such as dust particles.
In the second situation Air Drag at High Speeds.
For objects moving at high speeds through air, such as airplanes, sky divers, cars, and
Baseballs, etc.
- Resistive Force Proportional to Object Speed
If we assume that the resistive force acting on an object moving through a liquid or gas
is proportional to the object’s speed, then the resistive force can be expressed as
where v is the velocity of the object and b is a constant whose value depends on the
properties of the medium and on the shape and dimensions of the object. If the object
is a sphere of radius r, then b is proportional to r. The negative sign indicates that R is
in the opposite direction to v.
Consider a small sphere of mass m released from rest in a liquid, as in Figure 6.15a.
Assuming that the only forces acting on the sphere are the resistive force.
- Air Drag at High Speeds
For objects moving at high speeds through air, such as airplanes, sky divers, cars, and
baseballs, the resistive force is approximately proportional to the square of the speed.
In these situations, the magnitude of the resistive force can be expressed as
Where p is the density of air, A is the cross-sectional area of the moving object measured
in a plane perpendicular to its velocity, and D is a dimensionless empirical quantity
called the drag coefficient. The drag coefficient has a value of about 0.5 for spherical objects
but can have a value as great as 2 for irregularly shaped objects
6.5 Numerical Modeling in Particle Dynamics
In general, we apply
the analytical method to a dynamics problem using the following procedure:
1. Sum all the forces acting on the particle to find the net force ∑F.
2. Use this net force to determine the acceleration from the relationship a = ∑F/m
3. Use this acceleration to determine the velocity from the relationship dv/dt = a.
4. Use this velocity to determine the position from the relationship dx/dt = v.
The Euler Method
In the Euler method for solving differential equations, derivatives are approximated
as ratios of finite differences.
It is convenient to set up the numerical solution to this kind of problem by numbering
the steps and entering the calculations in a table. Table 6.3 illustrates how to do this in an orderly way.
One advantage of the Euler method is that the dynamics is not obscured—the
fundamental relationships between acceleration and force, velocity and acceleration,
and position and velocity are clearly evident.
The Euler method is completely reliable for infinitesimally small time increments,
but for practical reasons a finite increment size must be chosen.
but unfortunately it is not easy to determine the accuracy of an Euler-method solution without aknowledge of the correct analytical solution.
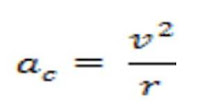







Tidak ada komentar:
Posting Komentar