The Center of Mass
In this section we describe the overall motion of a mechanical system in terms of a special point called the center of mass of the system. The mechanical system can be either a group of particles, such as a collection of atoms in a container, or an extended object, such as a gymnast leaping through the air. We shall see that the center of mass of the system moves as if all the mass of the system were concentrated at that point. Furthermore, if the resultant external force on the system is ∑ Feks and the total mass of the system is M, the center of mass moves with an acceleration given by a = ∑Feks/M. That is, the system moves as if the resultant external force were applied to a single particle. of mass M located at the center of mass. This behavior is independent of other motion, such as rotation or vibration of the system. This is the particle model.
The center of mass of the pair of particles described in Figure is located on the x axis and lies somewhere between the particles. Its x coordinate is given by
We can extend this concept to a system of many particles with masses mi in three dimensions. The x coordinate of the center of mass of n particles is defined to be
Although locating the center of mass for an extended object is somewhat more cumbersome than locating the center of mass of a system of articles, the basic ideas we have discussed still apply. We can think of an extended object as a system containing a large number of particles. The particle separation is very small, and so the object can be considered to have a continuous mass distribution. By dividing the object into elements of mass (mi with coordinates xi , yi , zi , we see that the x coordinate of the center of mass is approximately
We can express the vector position of the center of mass of an extended object in the form
The center of mass of any symmetric object lies on an axis of symmetry and on any plane of symmetry. For example, the center of mass of a uniform rod lies in the rod, midway between its ends. The center of mass of a sphere or a cube lies at its geometric center. Because an extended object is a continuous distribution of mass, each small mass element is acted upon by the gravitational force. The net effect of all these forces is equivalent to the effect of a single force Mg acting through a special point, called the center of gravity. If g is constant over the mass distribution, then the center of gravity coincides with the center of mass. If an extended object is pivoted at its center of gravity, it balances in any orientation.
Motion of a System of Particles
Assuming M remains constant for a system of particles, that is, no particles enter or leave the system, we obtain the following expression for the velocity of the center of mass of the system:
total linear momentum of the system equals the total mass multiplied by the velocity of the center of mass. In other words, the total linear momentum of the system is equal to that of a single particle of mass M moving with a velocity vCM. If we now differentiate Equation 9.34 with respect to time, we obtain the acceleration of the center of mass of the system:
The forces on any particle in the system may include both external forces (from outside the system) and internal forces (from within the system). However, by Newton’s third law, the internal force exerted by particle 1 on particle 2, for example, is equal in magnitude and opposite in direction to the internal force exerted by particle 2 on particle 1. Thus, when we sum over all internal forces in Equation 9.37, they cancel in pairs and we find that the net force on the system is caused only by external forces. Thus, we can write Equation 9.37 in the form
That is, the net external force on a system of particles equals the total mass of the system multiplied by the acceleration of the center of mass. The center of mass of a system of particles of combined mass M moves like an equivalent particle of mass M would move under the influence of the net external force on the system.
Finally, we see that if the net external force is zero, then from Equation 9.38 it follows that
That is, the total linear momentum of a system of particles is conserved if no net external force is acting on the system. It follows that for an isolated system of particles, both the total momentum and the velocity of the center of mass are constant in time
Rocket Propulsion
The operation of a rocket depends upon the law of conservation of linear momentum as applied to a system of particles, where the system is the rocket plus its ejected fuel .
A rocket moves in free space, its linear momentum changes when some of its mass is released in the form of ejected gases. Because the gases are given momentum when they are ejected out of the engine, the rocket receives a compensating momentum in the opposite direction. Therefore, the rocket is accelerated as a result of the “push,” or thrust, from the exhaust gases. In free space, the center of mass of the system (rocket plus expelled gases) moves uniformly, independent of the propulsion process.
This is the basic expression for rocket propulsion. First, it tells us that the increase in rocket speed is proportional to the exhaust speed ve of the ejected gases. Therefore, the exhaust speed should be very high. Second, the increase in rocket speed is proportional to the natural logarithm of the ratio Mi/Mf . Therefore, this ratio should be as large as possible, which means that the mass of the rocket without its fuel should be as small as possible and the rocket should carry as much fuel as possible.
The thrust on the rocket is the force exerted on it by the ejected exhaust gases. We can obtain an expression for the thrust from Equation 9.40:
This expression shows us that the thrust increases as the exhaust speed increases and as the rate of change of mass (called the burn rate) increases.















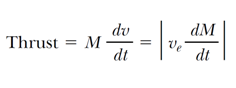
Tidak ada komentar:
Posting Komentar